Simulating a Centrifuge Test
Example Provided by: Antonios Vytiniotis, MIT
This article describes the basic OpenSees features needed for the simulation of vertically propagating shear waves in a scale model in a centrifuge. GID has been used for pre- and post- processing. For relatively simple configurations (even the one used in this paradigm) a pre-processor might not be needed, but a post-processor is necessary to visualize field output results. For every presented feature an example command is excerpted from the example tcl file and explained in detail. This tutorial does not explain though in every detail all the options associated in the various commands used. For this, the reader is directed to the OpenSees manual (the most recent is the on-line version of it). The commands and features used in this analysis have been tested with OpenSees versions 1.74, 1.75 and 2.0 but should also work for newer versions too. In case an example does not work, I would be obliged to hear about possible problems at avytin [at] mit . edu.
This manual explains how one can create a .tcl file that could be read and executed by the OpenSees interpreter. Notice should be taken that OpenSees is dimensionless, so the user must make sure that he uses a consistent system of units (e.g. SI).
Once an example.tcl file has been created, the user can then simply run OpenSees.exe, and in turn, write in the command line of the interpreter "source example.tcl" to run his analysis.
Simulated Geometry
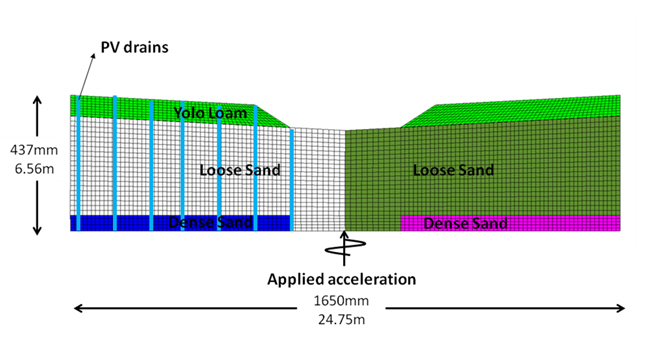
The centrifuge model geometry that we need to simulate is shown below. The model consists of two blocks of dense sand. On top of this lies a layer of loose liquefiable sand and on the top there are two facing slopes of Yolo Loam. The right hand side is treated with earthquake drains (PV-Drains) to accelerate the dissipation of excess pore pressure. An acceleration pattern is applied on the bottom of the model.
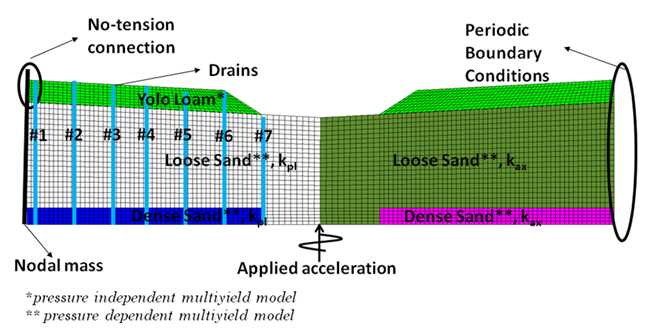
In the figure below, the most important finite element modelling features used in OpenSees are presented. These are explained in more detail in the next sections.
Elements Used
The elements used in this simulation are described in this section.
The Yolo Loam layer is simulated using total stress analysis with 4-noded quad elements. This element can be used to perform drained analysis, total stress analysis, and undrained analysis when coupled with the FluidSolidPorousMaterial material wrapper. An example of this command taken from the example's code is:
element quad 1 2327 2351 2326 2302 1.0 "PlaneStrain" 1 $press 1.3 $gravX $gravY'''
This command defines a planestrain quad element with id 1, that connects the nodes 2327, 2351, 2326, and 2302. The element has an out-of-plane width of 1 unit. The mechanical behavior is prescribed by material 1. The hydrostatic pressure of the element is the value of press. The total density of the material in the quad element is 1.3. The gravitational components in both directions are defined by the values of the parameters gravX and gravY.
The sand layer is simulated using 4-noded quadUP elements. These elements have three degrees of freedom per node: two for displacements, and one for pore pressure. It is important to keep in mind that the velocity, and not the displacement, of the 3rd DOF is the pore pressure, when requesting output or applying pore pressure conditions on the model. These elements can be used to model coupled pore pressure displacement analysis following the u-p formulation. Since they are four-noded they are expected not to perform very well in situations where they simulate incompressible behavior (e.g. undrained conditions). For completely undrained conditions the previously mentioned quad elements should be used together with the FluidSolidPorousMaterial material wrapper. An example how to define a quadUP element is:
element quadUP 417 4190 4191 4200 4199 1.0 3 $bulk 1. [expr 0.0003/9.81/1.] [expr 0.0003/9.81/1.] $gravX $gravY $press
This command creates a 4-noded planestrain quadUP element with id 417 that connects the nodes 4190, 4191, 4200, 4199. The element has a out-of-plane width of 1 unit. The mechanical behavior is prescribed by material 3. The bulk modulus of the pore fluid is the value of the variable bulk. The fluid mass density is 1. The hydraulic conductivity is k=0.0003. The gravitational components are defined by the values of the parameters gravX and gravy. The element also has a hydrostatic compression equal to the value of the variable press.
The soil material on the Yolo loam layer, where the effective stresses are small, should be able to disconnect from the laminar box. In order for this behavior to be modeled correctly, a zeroLength element should be defined. A zeroLength element connects two nodes that have the same, or almost the same coordinates according to an internally pre-specified threshold. The mechanical properties of this connection are defined by a uniaxial material which is attached to the zeroLength element. A sample definition of this type of element is:
element zeroLength 3933 4205 4221 -mat 7 7 -dir 1 2
This command creates a zeroLength element with id 3933 that connects the nodes 4205 and 4221. The mechanical behavior of this connection is prescribed by the uniaxial material 7 in direction 1 and by the same material in direction 2.
Materials Used
In this model, there are two types of materials being used. The first type are the continuum material models, referred to as nDMaterial, that are used to simulate the mechanical behaviour of sand, and they are attached to continuum elements. The second type are the uniaxial material elements that are attached either to ZeroLength elements, or to one-dimensional elements (e.g. beams or trusses). If they are attached to ZeroLength elements then their properties are used to simulate the force-displacement behaviour. If they are attached to one-dimensional elements then they simulate the stress-strain behaviour of the material in the element.
The Yolo Loam is modeled using a PressureIndependMultiYield material. This material exhibits plasticity only on the deviatoric stress space. It can be used to model the behavior of pressure independent materials, such as clays under usual states of stress (or clay-type material, such as Yolo Loam in this case). An example definition of the PressureIndependMultiyield model is:
nDMaterial PressureIndependMultiYield 1 2 1.37 13000 65000 6. .1
This command creates a PressureIndependMultiYield nDMaterial with tag 1, which is going to be used in a two-dimensional space. The material has a density of 1.37, a reference shear modulus of 13 000, a reference bulk modulus of 65 000, a cohesion of 6, and a peak shear strain parameter of 0.1.
The Sand layer is modeled using a PressureDependMultiYield02 nDMaterial model. This material allows for stress level dependent behavior, and shear induced volumetric strains, being able to model cyclic mobility and liquefaction. An example definition of this material is:
nDMaterial PressureDependMultiYield02 2 2 2.07 130000 260000 36.5 .1 80 0.5 26. 0.013 0.0 0.3 0.0
This command creates a PressureDependMultiYield02 nDMaterial Model with tag 2, which is going to be used in a two-dimensional space. The material has a total density of 2.07, a reference shear modulus of 130 000, a reference bulk modulus of 260 000, a friction angle of 36.5, a peak shear strain of 0.1, a reference pressure of 80, a pressuredependence coefficient of 0.5, a phase transformation angle of 26, a contraction1 parameter of 0.013, a contraction3 parameter of 0.0, a dilation1 parameter of 0.3, and dilation3 parameter of 0.0.
The connection between the quad soil elements of the top soil layer (Yolo Loam) with the box is modeled using a no tension material. In order for the analysis to converge more easily we couple in parallel the no-tension material with an elastic material of very small elastic modulus. An example of defining an elastic uniaxial material is:
uniaxialMaterial Elastic 9 10
which defines a linear Elastic uniaxialMaterial with id 9, and elastic modulus (E) of 10.
An example of defining an elastic no-tension material is:
uniaxialMaterial ENT 8 1000000000
which defines an ENT (Elastic-No-Tension) uniaxialMaterial with id 8, and an elastic modulus (E) of 1 000 000 000.
In order to combine the above two materials in parallel a Parallel uniaxialMaterial object should be defined:
uniaxialMaterial Parallel 7 8 9
which defines a Parallel uniaxialMaterial with id 7, where uniaxialMaterial 8 and uniaxialMaterial 9 behave as two springs in parallel.
Treatment of Boundary Conditions
Bottom Boundary Conditions
The bottom of the model is fixed in such a way that no movement is allowed on the vertical and horizontal direction. The pore pressure is allowed to fluctuate freely, which means that there is no drainage on the bottom. An example of a fixity command that fixes direction 1 (x), 2 (y), and leaves direction 3 (pore pressure) free is:
fix 925 1 1 0
Side Boundary Conditions
The displacements of the model on the sides at the level of the dense sand and the loose sand layers are fixed with periodic boundary conditions; each side has the same displacement with the other side. The command below ties the first and the second degree of freedom (DOF) of elements 58 and 4148.
equalDOF 58 4148 1 2
The nodes on the Yolo Loam level are connected at first with nodes with the same coordinates (representing the laminar box) with ENT zeroLength elements and, these nodes are connected with equalDOF objects with nodes on the other side of the box (periodic boundaries).
Earthquake Drain Pore Pressure Conditions
The drainage system is modelled as perfect drains; fixed pore pressure conditions are applied to them throughout the analysis. A pore pressure condition can be specified using the Timeseries command (to specify the behaviour of the condition vs. Time) and the MultipleSupport groundmotion command to specify the node and DOF to which the Timeseries applies at.
The code below is used to specify the pore pressure at a point on the top of the EQ-drain:
set Timeseries64 "Constant -factor 0.4495"
pattern MultipleSupport 3 {
...
groundMotion 64 Plain -vel $Timeseries64
imposedMotion 64 3 64
...
}
The command creates a MultipleSupport pattern object with id 3, an object that allows users to define a fixed acceleration, velocity, or displacement of a specific DOF on a specific node. It then applies the conditions for every node. For every node we specify a imposedMotion object that attaches a specified groundMotion to the node. In this case, we create a groundMotion object with id 64 that is Plain, of type velocity, and has as arguments the value of the parameter Timeseries64 (Constant timeseries of value 0.4495). By means, of this set of commands we specify that the pore pressure in node 64 has a value of 0.4495. If applying this boundary condition does not work, one should specify acceleration, velocity, and displacement boundary conditions all at the same time, at the same node.
Top Pore Pressure Conditions
When one defines the ground water level to be above the ground surface (and applies the relevant pore pressure conditions on top), one needs also to apply the hydrostatic pressure of the water normal to the ground surface in order for the effective stresses to be computed correctly.
The code below shows the application of pore pressure 5.6658 at node 1761.
set Timeseries1761 "Constant -factor 5.6658"
pattern MultipleSupport 3 {
...
groundMotion 31761 Plain -vel $Timeseries1761
imposedMotion 1761 3 31761
...
}
In order to match the effective stresses on the top of the layer in the middle of the central channel, where the ground water level is above the soil surface, one should also specify the loads applied due to the water weight to the soil surface with the following command:
set Timeseries "Constant -factor -1.8"
pattern Plain 4 $Timeseries {
...
load 1561 0. .1 0.
...
}
The above command specifies a vertical load of -0.18 on the node 1561. By applying these loads we make sure that the effective stresses at the ground surface are exactly zero.
Also, the shear rings of the laminar box have a specific mass. We apply concentrated mass at the x direction on the side nodes of the model. The following command specifies a nodal mass of the value of 0.01015 at the node 58:
mass 58 0.01015 0 0
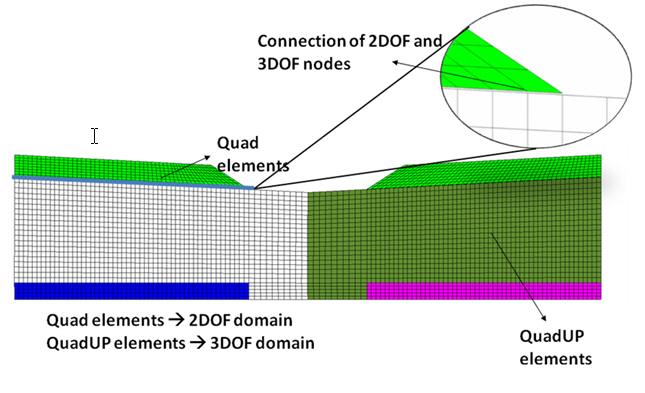
In this model there are two types of domains, the two-DOF domain where the quad elements and their respective nodes have been created, and the three-DOF domain where the quadup elements and their respective nodes have been created. In order for the two domains to be connected the nodes on the common boundaries of the two domains are connected with equalDOF objects, as shown below.
In the example below the horizontal and vertical displacement DOFs of node 39 having two DOFs is connected to the node 40 having 3 DOFs.
equalDOF 40 39 1 2
Figure C Connection of the 2DOF to the 3DOF domains
Solution Procedure
The typical solution procedure used is:
- Use elastic material for the entire model, turn on the gravity and solve the static case. The way this is performed is by solving a coupled transient analysis with a very large time-step, and very large gamma (1.5). The gamma parameter of the Newmark integrator controls the numerical damping (not the Rayleigh damping). If gamma=0.5 then there is no numerical damping. A value of gamma=1.6 makes sure that the initial dynamic transient will dissipate very quickly. The very large time-step (dt=5.e5) is used to make sure that the analysis is drained, and that any initial excess pore pressures have dissipated. The large time-step also helps the dissipation of the initial transient. In the elastic analysis one can choose the Poisson's ratio in such a way that the initial K0 value is predicted correctly.
- After the elastic step, when all the initial transients and excess pore pressures have dissipated, the material is switched to an elasto-plastic state, and a similar analysis with large gamma and large time-step is performed.
- After the elasto-plastic gravity step the analysis object is destroyed, and the time is reset to zero. Then the dynamic analysis is executed.
This is a typical procedure used for the UCSD soil models. For other models it might not be possible to run the elastic step, so one should start directly with the second step of the analysis. In that case, the user should pay extra attention to (1) make the analysis converge correctly to the initial state, and (2) correctly track and assign the model state parameters.
Elastic Gravity Step
The models created by UCSD (PressureDependMultiYield, PressureInDependMultiYield, PressureDependMultiYield02) have been implemented with an internal switch parameter that allows them to behave either as linear elastic, elasto-plastic, or elastic pressure-dependent. In order to switch this type of material to an elastic state for the elastic part of the gravity loading the following command is issued:
updateMaterialStage -material 1 -stage 0
The command above specifies that material 1 should behave according to stage flag 0, which is a linear elastic state.
Next, the analysis objects need to be defined:
set gamma 1.6 # create the SOE, ConstraintHandler, Integrator, Algorithm and Numberer integrator Newmark $gamma [expr pow($gamma+0.5, 2)/4] 0.00 0.0 0.00 0.0 test EnergyIncr 1.0e-8 400 1; constraints Transformation algorithm Newton numberer RCM system ProfileSPD analysis Transient
The above command creates a Newmark integrator with gamma=1.6. Beta b=(gamma+0.5)2/4 is chosen because this value provides unconditional stability of the integration algorithm. The Newmark integrator has been shown to produce spurious oscillations in the results, so it is advisable to use the HHT integrator, when possible. On the other hand, the choice of an integrator is also judged on a case to case basis based on its convergence and speed.
The test to judge when convergence has been achieved is based on increments of energy. This is a good criterion in an elasto-plastic problem where increments of displacement can be really large during yielding.
The constraint handler is set as the transformation handler, after recommendations from the creators of the quadUP elements when one is applying pore pressure boundary conditions.
The algorithm selected is a Newton algorithm. It is a robust and simple algorithm with asymptotically quadratic rate of convergence. The Newton-Raphson algorithms are computationally expensive and are known to suffer from residual flip flop due to sudden changes in the tangent stiffness matrix. Linear convergence can be achieved with ModifiedNewton algorithms. In principle, the fastest implemented algorithm should be the KrylovNewton, so it should be preferred, but there are situations that it might not converge to a solution.
The system used is a ProfileSPD. The Jacobian matrix of frictional materials is not symmetric, but in many situations ignoring the non-symmetric elements can help improve performance without significant differences in the results. A good alternative would be an unsymmetric system like UmfPack.
Finally the analysis object selected is Transient. This gives the ability to implement our own code to define the analysis sub-incrementation.
Elasto-plastic Gravity Step
The same analysis objects are used for the elasto-plastic gravity step. The materialstage is updated to simulate elastoplastic response (one more time this applies only to PressureDependMultiYield, PressureDependMultiYield02, PressureInDependMultiYield models) :
updateMaterialStage -material 1 -stage 1
The command above specifies that material 1 should behave according to stage flag 1, which is a elasto-plastic state.
Elasto-plastic Dynamic Step
The load is applied using a very simple command:
pattern UniformExcitation 1 1 -accel $Timeseries_1;
This command creates a UniformExcitation object with tag 1, which applies to all the nodes in direction 1(x), an acceleration pattern (-accel) defined by the value of the parameter $Timeseries_1. If one defines more than one objects of this type, the results would be superimposed. The output of this analysis would be relative relative to the displacement of these nodes (i.e. the nodes fixed in direction 1 will have as output zero accelerations).
The analysis objects need to be defined:
set gamma 0.65 # create the SOE, ConstraintHandler, Integrator, Algorithm and Numberer integrator Newmark $gamma [expr pow($gamma+0.5, 2)/4] 0.00 0.0 0.0002 0.0 constraints Transformation algorithm Newton numberer RCM system ProfileSPD analysis Transient
The above command creates a Newmark integrator with gamma=0.65, which adds some minor numerical damping. Also, some minor Rayleigh damping is added. This is a good compromise between accuracy and numerical stability for this part of the analysis. The rest of the analysis is kept the same with the gravity analysis.
During the analysis recorder objects are used to track pore pressures, effective stresses, accelerations, and displacements.
set r_1 [recorder Node -file output_disp_11.txt -nodeRange 1 4204 -time -dT 0.05 -dof 1 2 disp] set r_2 [recorder Node -file output_accel_11.txt -nodeRange 1 4204 -time -dT 0.05 -dof 1 2 accel] set r_3 [recorder Node -file output_pore_11.txt -nodeRange 1 4204 -time -dT 0.05 -dof 3 vel] set r_4 [recorder Element -file stress_1_11.txt -time -dT 0.05 -eleRange 1 3932 material 1 stress] set r_8 [recorder Element -file strain_1_11.txt -time -dT 0.05 -eleRange 1 3932 material 1 strain]
In the above code, five types of recorders are illustrated, the displacement, the acceleration, the pore pressure, the stress, and the strain recorders. We note that the strain and stress values are extracted from the material class, so different implementations of materials might not include these recorders. Parameters r_1, r_2, r_3, r_4 have handles to the created recorder objects.
Later in the analysis we can conveniently destroy the recorders:
remove recorder $r_1
The above command destroys the recorder object with tag the value of the parameter r_1. This is done to store different parts of the analysis to different output files.
Next, a sample of the code that allows for control on the incrementation of the solution procedure is presented:
set ok 0
set currentTime 0.0
set i_extr_nl 0.0
set dt 0.005
set i_suc 0
set disp_incr 1.0e-5
set iter 30
algorithm Newton
while {$currentTime < 13.} {
test EnergyIncr $disp_incr $iter 2;
set ok [analyze 1 $dt]
set currentTime [getTime]
puts "$ok dt=$dt Disp_incr=$disp_incr #Iter=$iter"
if {$ok ==0} {
set i_suc [expr $i_suc+1]
if {$disp_incr>1e-3} {
set i_extr_nl [expr $i_extr_nl+1]
}
if {$i_suc>10} {
set disp_incr [expr $disp_incr/2]
if {$disp_incr<1e-6} {
set disp_incr 1e-6
}
if {$dt<0.0005} {
set iter 30
}
}
if {$i_suc>20} {
set dt [expr $dt*2]
if {$dt>0.05} {
set dt 0.05
}
}
}
if {$ok !=0} {
set dt [expr $dt/2]
if {$i_suc==0} {
set disp_incr [expr $disp_incr*2]
if {$disp_incr>0.005} {
set disp_incr 0.005
}
}
if {$dt<0.0005} {
set iter 200
}
set i_suc 0
}
}
In the above algorithm we try to evaluate a step using an initial time-step. In case of non-convergence the algorithm changes the convergence criteria and the time-step so that the analysis converges. In case of convergence, the algorithm increases the time-step and tightens the convergence criteria up to some pre-specified limits. This part of the code should always be tailored according to accuracy and speed needs of every analysis.
Results
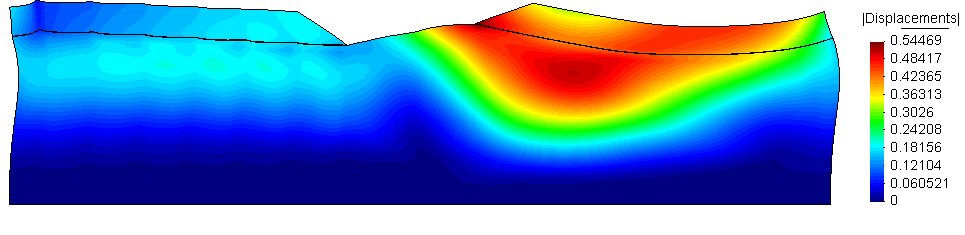
Three phases of shaking and dissipation are allowed in the happen in the model. A full analysis of the example file, will take around a day, depending on the processor speed. A sample output, after the end of all the shaking and dissipation of all the accumulated excess pore pressure, produced with GiD is shown below.