Main Page Class Hierarchy Alphabetical List Compound List File List Compound Members File Members
TransientIntegrator Class Reference#include <TransientIntegrator.h>
Inheritance diagram for TransientIntegrator::
List of all members.
Detailed Description
TransientIntegrator is an abstract subclass of IncrementalIntegrator. A subclass of it is used when performing a nonlinear transient analysis of the problem using a direct integration method. The TransientIntegrator class redefines the {formTangent()} method of the IncrementalIntegrator class and it defines a new method {newStep()} which is invoked by the DirectIntegrationAnalysis class at each new time step. \
In nonlinear transient finite element problems we seek a solution (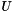
, 
, 
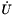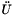) to the nonlinear vector function
\begin{equation} \R(U,Ud, Udd) = \P(t) - \F_I(Udd) - \F_R(U, Ud) = \zero \label{femGenForm} \end{equation}
The most widely used technique for solving the transient non-linear finite element equation, equation~\ref{femGenForm}, is to use an incremental direct integration scheme. In the incremental formulation, a solution to the equation is sought at successive time steps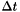 
apart.
\begin{equation} \R(U_{n \Delta t},Ud_{n \Delta t}, Udd_{n \Delta t}) = \P(n \Delta t) - \F_I(Udd_{n \Delta t}) - \F_R(U_{n \Delta t}, Ud_{n \Delta t}) \label{fullTimeForm} \end{equation}
For each time step, t, the integration schemes provide two operators, 
and 
, to relate the velocity and accelerations at the time step as a function of the displacement at the time step and the response at previous time steps:
\begin{equation} \dot U_{t} = {\I}_1 (U_t, U_{t-\Delta t}, \dot U_{t-\Delta t}, \ddot U_{t - \Delta t}, U_{t - 2\Delta t}, \dot U_{t - 2 \Delta t}. ..., ) \label{I1} \end{equation}
\begin{equation} \ddot U_{t} = {\I}_2 (U_t, U_{t-\Delta t}, \dot U_{t-\Delta t}, \ddot U_{t - \Delta t}, U_{t - 2\Delta t}, \dot U_{t - 2 \Delta t}. ..., ) \label{I2} \end{equation}
These allow us to rewrite equation~\ref{fullTimeForm}, in terms of a single response quantity, typically the displacement:
\begin{equation} \R(U_t) = \P(t) - \F_I(Udd_t) - \F_R(U_t, Ud_t) \label{genForm} \end{equation}
The solution of this equation is typically obtained using an iterative procedure, i.e. making an initial prediction for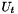 
, denoted 
a sequence of approximations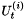 
, 
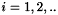is obtained which converges (we hope) to the solution
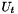. The most frequently used iterative schemes, such as Newton-Raphson, modified Newton, and quasi Newton schemes, are based on a Taylor expansion of equation~\ref{genForm} about
:
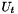\begin{equation} \R(U_{t}) = \R(U_{t}^{(i)}) + \left[ {\frac{ -
tial \R}{\partial U_t} \vert}_{U_{t}^{(i)}}\right]
-
\left( U_{t} - U_{t}^{(i)} \right) \end{equation}
\R(U_{t}) = \P (t)
- \f_{I} \left( \ddot U_{t}^{(i)} \right) - \f_{R} \left( \dot U_{t}^{(i)}, U_{t}^{(i)} \right)
\begin{equation}
\left[ \M^{(i)} {\I}_2' + \C^{(i)} {\I}_1' + K^{(i)} \right] \left( U_{t} - U_{t}^{(i)} \right) \label{femGenFormTaylor} \end{equation}
To start the iteration scheme, trial values for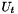
, 
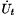and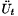 
are required. These are obtained by assuming 
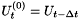. The 
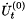and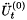 
can then be obtained from the operators for the integration scheme. \
Subclasses of TransientIntegrators provide methods informing the FE\_Element and DOF\_Group objects how to build the tangent and residual matrices and vectors. They also provide the method for updating the response quantities at the DOFs with appropriate values; these values being some function of the solution to the linear system of equations. \
}
Definition at line 150 of file TransientIntegrator.h.
Constructor & Destructor Documentation
|
TransientIntegrator::TransientIntegrator (
|
int classTag )
|
|
|
TransientIntegrator::~TransientIntegrator (
|
) [virtual]
|
|
Member Function Documentation
|
int TransientIntegrator::formEleResidual (
|
FE_Element * theEle ) [virtual]
|
|
|
|
Called upon by the FE\_Element {theEle} to determine it's contribution to the rhs of the equation. The following are invoked before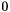 
is returned. \begin{tabbing} while \= \+ while \= while \= \kill theEle-
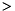zeroResidual()
Reimplemented from IncrementalIntegrator.
Reimplemented in HHT, and Newmark.
Definition at line 107 of file TransientIntegrator.cpp. |
|
int TransientIntegrator::formNodUnbalance (
|
DOF_Group * theDof ) [virtual]
|
|
|
|
Called upon by the DOF\_Group {theDof} to determine it's contribution to the rhs of the equation. The following are invoked before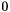
is returned. \begin{tabbing} while \= \+ while \= while \= \kill theDof-
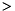zeroUnbalance()
Reimplemented from IncrementalIntegrator.
Reimplemented in HHT, and Newmark.
Definition at line 115 of file TransientIntegrator.cpp. |
|
int TransientIntegrator::formTangent (
|
int statFlag ) [virtual]
|
|
|
|
Invoked to form the structure tangent matrix. The method is rewritten for this class to include inertia effects from the nodes. The method iterates over both the FE\_Elements and DOF\_Groups invoking methods to form their contributions to the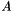 
matrix of the LinearSOE and then adding these contributions to the
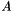matrix. The method performs the following: \begin{tabbing} while \= \+ while \= while \= \kill theSysOfEqn.zeroA();
Reimplemented from IncrementalIntegrator.
Definition at line 61 of file TransientIntegrator.cpp. |
|
int TransientIntegrator::initialize (
|
void ) [inline, virtual]
|
|
|
int TransientIntegrator::newStep (
|
double deltaT ) [pure virtual]
|
|
The documentation for this class was generated from the following files:
|
Copyright