ZeroLengthContactNTS2D
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a zeroLengthContactNTS2D element object. This is a Node-To-Segment (NTS) frictional contact element used in two dimensional analysis for contact between elements with 2 DOF nodes.
| element zeroLengtContactNTS2D $eleTag -cNdNum $cNdNum -rNdNum $rNdNum -Nodes $Nodes $Kn $kt $phi |
| $eleTag | unique element object tag |
| $cNdNum | Number of Constrained Nodes |
| $rNdNum | Number of Retained nodes |
| $Nodes ... | Constrained and Retained node tags respectively |
| $Kn | Penalty in normal direction |
| $Kt | Penalty in tangential direction |
| $phi | Friction angle in degrees |
NOTES:
- The contact element is node-to-segment (NTS) contact. The relation follows Mohr-Coulomb frictional law: <math>T = N \times tan(\phi)</math>, where <math>T</math> is the tangential force, <math>N</math> is normal force across the interface and <math>\phi\,\!</math> is friction angle.
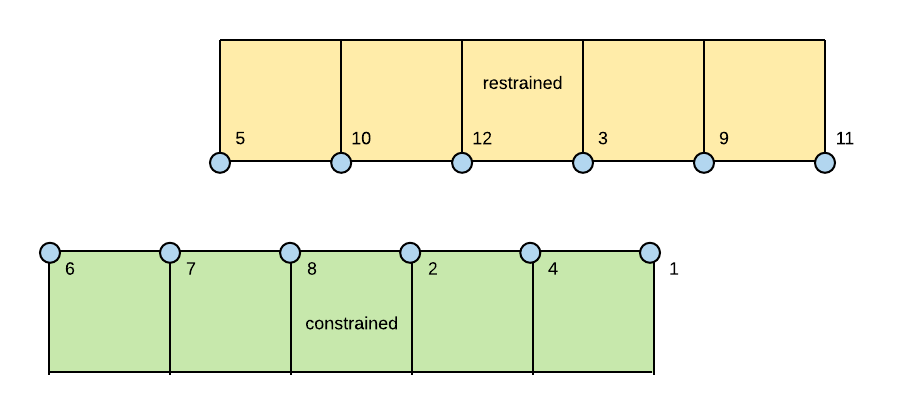
- For 2D contact, constrained nodes and retained nodes must be 2 DOF and notice that the constrained and retained nodes must be entered in counterclockwise order.
- The resulting tangent from the contact element is non-symmetric. Switch to the non-symmetric matrix solver if convergence problem is experienced.
- As opposed to node-to-node contact, predefined normal vector for node-to-segment (NTS) element is not required because contact normal will be calculated automatically at each step.
- contact element is implemented to handle large deformations.
EXAMPLE:
element zeroLengthContactNTS2D 1 -cNdNum 6 -rNdNum 6 - Nodes 5 10 12 3 9 11 1 4 2 8 7 6 1e8 1e8 16
Example 1:
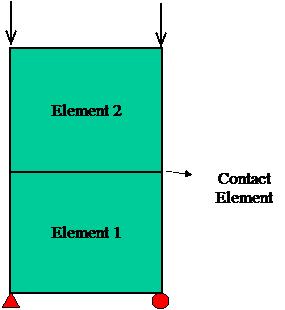
This example simply shows the two quadrilateral elements in normal contact. The top element is in normal downward uniform force. The Tcl script of this example can be found here.
Example 2:
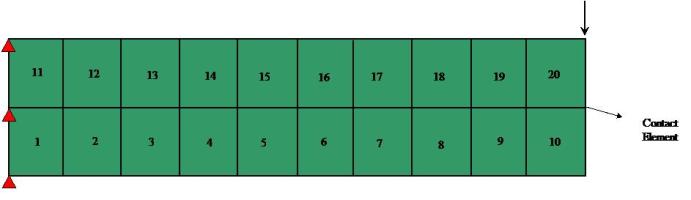
This example shows two cantilever beams in contact. The beams were modeled using four-node quadrilateral elements and the end of top beam was subjected to a linearly increasing displacement. The Tcl scripts for this example can be found here.
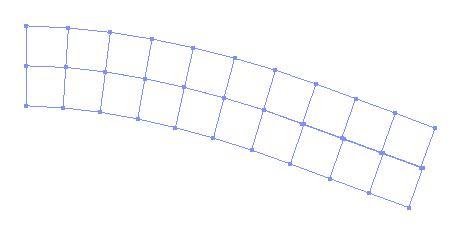
The following Figure shows the deflections of the two beams.
REFERENCES:
- P. Wriggers, V.T. Vu and E. Stein, Finite-element formulation of large deformation impact–contact problems with friction, Comput. Struct. 37 (1990), pp. 319–331.
- Peter Wriggers. Computational Contact Mechanics. John Wiley & Sons Ltd. Chichester, 2002.
Code Developed by: Roozbeh G. Mikola, UC Berkeley and N. Sitar, UC Berkeley