Single Friction Pendulum Bearing Element
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
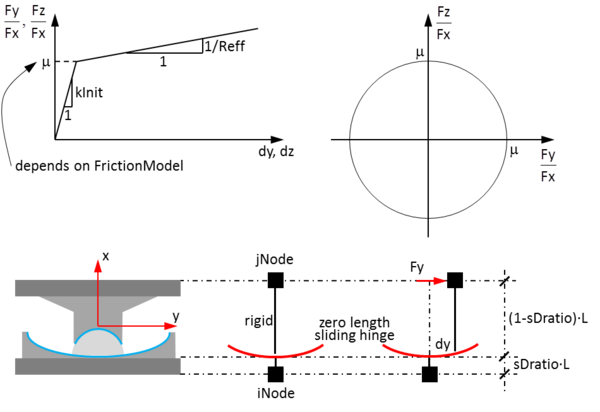
This command is used to construct a singleFPBearing element object, which is defined by two nodes. The iNode represents the concave sliding surface and the jNode represents the articulated slider. The element can have zero length or the appropriate bearing height. The bearing has unidirectional (2D) or coupled (3D) friction properties (with post-yield stiffening due to the concave sliding surface) for the shear deformations, and force-deformation behaviors defined by UniaxialMaterials in the remaining two (2D) or four (3D) directions. To capture the uplift behavior of the bearing, the user-specified UniaxialMaterial in the axial direction is modified for no-tension behavior. By default (sDratio = 0.0) P-Delta moments are entirely transferred to the concave sliding surface (iNode). It is important to note that rotations of the concave sliding surface (rotations at the iNode) affect the shear behavior of the bearing. To avoid the introduction of artificial viscous damping in the isolation system (sometimes referred to as "damping leakage in the isolation system"), the bearing element does not contribute to the Rayleigh damping by default. If the element has non-zero length, the local x-axis is determined from the nodal geometry unless the optional x-axis vector is specified in which case the nodal geometry is ignored and the user-defined orientation is utilized.
For a two-dimensional problem:
| element singleFPBearing $eleTag $iNode $jNode $frnMdlTag $Reff $kInit -P $matTag -Mz $matTag <-orient $x1 $x2 $x3 $y1 $y2 $y3> <-shearDist $sDratio> <-doRayleigh> <-mass $m> <-iter $maxIter $tol> |
For a three-dimensional problem:
| element singleFPBearing $eleTag $iNode $jNode $frnMdlTag $Reff $kInit -P $matTag -T $matTag -My $matTag -Mz $matTag <-orient <$x1 $x2 $x3> $y1 $y2 $y3> <-shearDist $sDratio> <-doRayleigh> <-mass $m> <-iter $maxIter $tol> |
| $eleTag | unique element object tag |
| $iNode $jNode | end nodes |
| $frnMdlTag | tag associated with previously-defined FrictionModel |
| $Reff | effective radius of concave sliding surface |
| $kInit | initial elastic stiffness in local shear direction |
| -P $matTag | tag associated with previously-defined UniaxialMaterial in axial direction |
| -T $matTag | tag associated with previously-defined UniaxialMaterial in torsional direction |
| -My $matTag | tag associated with previously-defined UniaxialMaterial in moment direction around local y-axis |
| -Mz $matTag | tag associated with previously-defined UniaxialMaterial in moment direction around local z-axis |
| $x1 $x2 $x3 | vector components in global coordinates defining local x-axis (optional) |
| $y1 $y2 $y3 | vector components in global coordinates defining local y-axis (optional) |
| $sDratio | shear distance from iNode as a fraction of the element length (optional, default = 0.0) |
| -doRayleigh | to include Rayleigh damping from the bearing (optional, default = no Rayleigh damping contribution) |
| $m | element mass (optional, default = 0.0) |
| $maxIter | maximum number of iterations to undertake to satisfy element equilibrium (optional, default = 20) |
| $tol | convergence tolerance to satisfy element equilibrium (optional, default = 1E-8) |
NOTE:
1) If the element has zero length and optional orientation vectors are not specified, the local element axes coincide with the global axes. Otherwise the local z-axis is defined by the cross product between the x- and y-vectors specified on the command line.
2) Because the friction force is affected by both the axial force and the slip rate, the element can be sensitive numerically. It is recommended that for dynamic analysis a smaller time step is being used than what would be used for a comparable structure with no isolators.
3) If there is uplift (and therefore impact) in the bearing element, it can be helpful to use an integration method that provides numerical damping. Providing some viscous damping for the material that is assigned to the axial direction can also be helpful in dissipating impact energy.
4) The valid queries to a single concave friction pendulum bearing element when creating an ElementRecorder object are 'force,' 'localForce,' 'basicForce,' 'localDisplacement,' 'basicDisplacement' and 'material $matNum matArg1 matArg2 ...' Where $matNum is the number associated with the material whose data is to be output.
EXAMPLES:
For a 2D single concave friction pendulum bearing: element singleFPBearing 1 1 2 1 34.68 250.0 -P 1 -Mz 2 -orient 0 1 0 -1 0 0;
- TestFPS2d_0.tcl models a rigid isolated mass and the bearing element has zero length. It also tests the different friction models.
- TestFPS2d_1.tcl models a rigid isolated mass and the bearing element has finite length.
- TestFPS2d_2.tcl models an isolated one story stick and the bearing element has finite length.
- TestFPS2d_3.tcl models an isolated one story one bay building and the bearing element has finite length.
- TestFPS2d_4.tcl models an isolated five story one bay building and the bearing element has finite length.
For a 3D single concave friction pendulum bearing: element singleFPBearing 1 1 2 1 34.68 250.0 -P 1 -T 2 -My 3 -Mz 4 -orient 0 0 1 -1 0 0;
- TestFPS3d_0.tcl models a rigid isolated mass and the bearing element has zero length. It also tests the different friction models.
- TestFPS3d_1.tcl models a rigid isolated mass and the bearing element has finite length.
- TestFPS3d_2.tcl models an isolated one story stick and the bearing element has finite length.
- TestFPS3d_3.tcl models an isolated one story one bay building and the bearing element has finite length.
- TestFPS3d_4.tcl models an isolated five story one bay building and the bearing element has finite length.
Download the GroundMotions.zip as a compressed file or download AllFPSExamples.zip as a compressed file.
Code Developed by: Andreas Schellenberg, University of California, Berkeley.