Pushover Analysis of 2-Story Moment Frame
Example posted by: Laura Eads, Stanford University
This example demonstrates how to perform a pushover (nonlinear static) analysis in OpenSees using a 2-story, 1-bay steel moment resisting frame. In the first model, the nonlinear behavior is represented using the concentrated plasticity concept with rotational springs. In the second model, the nonlinear behavior is represented using the distributed plasticity concept where the plastic behavior occurs over a finite length. The rotational behavior of the plastic regions in both models follows a bilinear hysteretic response based on the Modified Ibarra Krawinkler Deterioration Model (Ibarra et al. 2005, Lignos and Krawinkler 2009, 2010). For this example, all modes of cyclic deterioration are neglected. A leaning column carrying gravity loads is linked to the frame to simulate P-Delta effects.
The files needed to analyze this structure in OpenSees are included here:
- The main files: pushover_concentrated.tcl and pushover_distributed.tcl
Supporting procedure files
- DisplayModel2D.tcl – displays a 2D perspective of the model
- DisplayPlane.tcl – displays a plane in the model
- rotSpring2DModIKModel.tcl – creates a bilinear rotational spring that follows the Modified Ibarra Krawinkler Deterioration Model (used in the concentrated model)
- rotSect2DModIKModel.tcl – creates a section with bilinear rotational response that follows the Modified Ibarra Krawinkler Deterioration Model and an elastic axial response (used in the distributed model)
- rotLeaningCol.tcl – creates a low-stiffness rotational spring used in a leaning column
All files are available in a compressed format here: pushover_example.zip
The rest of this example describes the models and compares their analysis results. The OpenSees models are also compared to an equivalent model built and analyzed using the commercial program SAP2000 (http://www.csiberkeley.com/products_SAP.html).
Model Description

Concentrated Plasticity Model Overview
The 2-story, 1-bay steel moment resisting frame is modeled with elastic beam-column elements connected by zeroLength elements which serve as rotational springs to represent the structure’s nonlinear behavior. The springs follow a bilinear hysteretic response based on the Modified Ibarra Krawinkler Deterioration Model. A leaning column with gravity loads is linked to the frame by truss elements to simulate P-Delta effects. An idealized schematic of the model is presented in Figure 1.

Distributed Plasticity Model Overview
The 2-story, 1-bay steel moment resisting frame is modeled using "beam with hinges" elements. Plastic hinge regions are assigned to the ends of these elements. The plastic regions have an elastic axial response and a bilinear rotational response based on the Modified Ibarra Krawinkler Deterioration Model. An idealized schematic of the model is presented in Figure 2.
Features Common to Both Models
A leaning column with gravity loads is linked to the frame by truss elements to simulate P-Delta effects.
To simplify this model, panel zone contributions are neglected and plastic hinges form at the beam-column joints, i.e., centerline dimensions are used. For an example that explicitly models the panel zone shear distortions and includes reduced beam sections (RBS), see Pushover and Dynamic Analyses of 2-Story Moment Frame with Panel Zones and RBS.
The units of the model are kips, inches, and seconds.
Basic Geometry
The basic geometry of the frame is defined by input variables for the bay width, height of the first story, and height of a typical (i.e. not the first) story. These values are set as WBay = 360”, HStory1 = 180”, and HStoryTyp = 144”. The leaning column line is located one bay width away from the frame. In addition to the nine beam-column joint nodes, there is one additional node for each spring, which connects the spring to the elastic element. This makes a total of 24 nodes in the structure for the concentrated plasticity model compared to 12 nodes in the distributed plasticity model.
Leaning Columns and Frame Links
The leaning columns are modeled as elastic beam-column elements. These columns have moments of inertia and areas about two orders of magnitude larger than the frame columns in order to represent aggregate effect of all the gravity columns (Aleaning column = 1,000.0 in2 and Ileaning column = 100,000.0 in4). The columns are connected to the beam-column joint by zeroLength rotational spring elements with very small stiffness values so that the columns do not attract significant moments. These springs are created using rotLeaningCol.tcl.
Truss elements are used to link the frame and leaning columns and transfer the P-Delta effect. The trusses have areas about two orders of magnitude larger than the frame beams in order to represent aggregate effect of all the gravity beams (Atruss = 1,000.0 in2) and can be assumed to be axially rigid.
Rotational Springs (Concentrated Plasticity Model)
The rotational springs capture the nonlinear behavior of the frame. As previously mentioned, the springs in the example employ a bilinear hysteretic response based on the Modified Ibarra Krawinkler Deterioration Model. Detailed information about this model and the modes of deterioration it simulates can be found in Ibarra et al. (2005) and Lignos and Krawinkler (2009, 2010).
In this example, the zeroLength spring elements connect the elastic frame elements to the beam-column joint nodes. The springs are created using rotSpring2DModIKModel.tcl.
Plastic Hinge Regions (Distributed Plasticity Model)
In this model the plasticity is distributed over a defined length. The axial and flexural responses of each plastic hinge region are defined as separate sections. The axial response is defined by an elastic section while the flexural response is defined by a uniaxial section using the bilinear material based on the Modified Ibarra Krawinkler Deterioration Model. The responses are combined into a single section using the section aggregator command. P-M interactions are neglected in this example as the axial loads are relatively low and are not expected to have a significant influence.
Plasticity Features Common to Both Models
The input parameters for the rotational behavior of the plastic hinges in both models are determined using empirical relationships developed by Lignos and Krawinkler (2010) which are derived from an extensive database of steel component tests. Alternatively, these input parameters can be determined using approaches similar to those described in FEMA 356 (http://www.fema.gov/library/viewRecord.do?id=1427), ATC-72 and ATC-76 (http://www.atcouncil.org/index.php?option=com_content&view=article&id=45&Itemid=54). In order to simplify the model, cyclic deterioration was ignored. This was accomplished by setting all of the “L” deterioration parameter variables to 1000.0, all of the “c” exponent variables to 1.0, and both “D” rate of cyclic deterioration variables to 1.0.
Stiffness Modifications to Elastic Frame Elements (Concentrated Plasticity Model)
Since a frame member is modeled as an elastic element connected in series with rotational springs at either end, the stiffness of these components must be modified so that the equivalent stiffness of this assembly is equivalent to the stiffness of the actual frame member. Using the approach described in Appendix B of Ibarra and Krawinkler (2005), the rotational springs are made “n” times stiffer than the rotational stiffness of the elastic element in order to avoid numerical problems and allow all damping to be assigned to the elastic element. To ensure the equivalent stiffness of the assembly is equal to the stiffness of the actual frame member, the stiffness of the elastic element must be “(n+1)/n” times greater than the stiffness of the actual frame member. In this example, this is accomplished by making the elastic element’s moment of inertia “(n+1)/n” times greater than the actual frame member’s moment of inertia.
Stiffness Modifications to the Plastic Hinges (Both Models)
In order to make the nonlinear behavior of the assembly match that of the actual frame member, the strain hardening coefficient (the ratio of post-yield stiffness to elastic stiffness) of the plastic hinge must be modified. If the strain hardening coefficient of the actual frame member is denoted <math>\alpha</math>s,mem and the strain hardening coefficient of the spring (or plastic hinge region) is denoted <math>\alpha</math>s,spring then <math>\alpha</math>s,spring = <math>\alpha</math>s,mem / (1 + n*(1 - <math>\alpha</math>s,mem))
Note that this is a corrected version of Equation B.5 from Ibarra and Krawinkler (2005).
Constraints
The frame columns are fixed at the base, and the leaning column is pinned at the base. To simulate a rigid diaphragm, the horizontal displacements of all nodes in a given floor are constrained to the leftmost beam-column joint node using the equalDOF command.
Masses
The mass is concentrated at the beam-column joints of the frame, and each floor mass is distributed equally among the frame nodes. The mass is assigned using the node command, but it could also be assigned with the mass command.
Loading
Gravity loads are assigned to the beam-column joint nodes using the nodal load command. Gravity loads tributary to the frame members are assigned to the frame nodes while the remaining gravity loads are applied to the leaning columns. The gravity loads are applied as a plain load pattern with a constant time series since the gravity loads always act on the structure.
In this example, lateral loads are distributed to the frame using the methodology of ASCE 7-10 (http://www.asce.org/Product.aspx?id=2147487569). Lateral loads are applied to all the frame nodes in a given floor. A plain load pattern with a linear time series is used for lateral load application so that loads increase with time.
Recorders
The recorders used in this example include:
- The drift recorder to track the story and roof drift histories
- The node recorder to track the base shear reaction history
- The element recorder to track the element forces in the first story columns as well as the moment and rotation histories of the springs in the concentrated plasticity model
To record the moment and rotation histories in the springs, the region command was used to assign all column springs to one group and all beam springs to a separate group, and the region was used as an input to the element recorder.
It is important to note that the recorders only record information for analyze commands that are called after the recorder commands are called. In this example, the recorders are placed after the gravity analysis so that the steps of the gravity analysis do not appear in the output files.
Analysis
The structure is first analyzed under gravity loads before the pushover analysis is conducted. The gravity loads are applied using a load-controlled static analysis with 10 steps. So that the gravity loads remain on the structure for all subsequent analyses, the loadConst command is used after the gravity analysis is completed. This command is also used to reset the time to zero so that the pushover starts from time zero.
The pushover analysis is performed using a displacement-controlled static analysis. In this example, the structure was pushed to 10% roof drift, or 32.4”. The roof node at Pier 1, node 13 in Figures 1 and 2, was chosen as the control node where the displacement was monitored. Incremental displacement steps of 0.01” were used. This step size was used because it is small enough to capture the progression of hinge formation and generate a smooth backbone curve, but not too small that it makes the analysis time unreasonable.
Results
Comparison of OpenSees Models
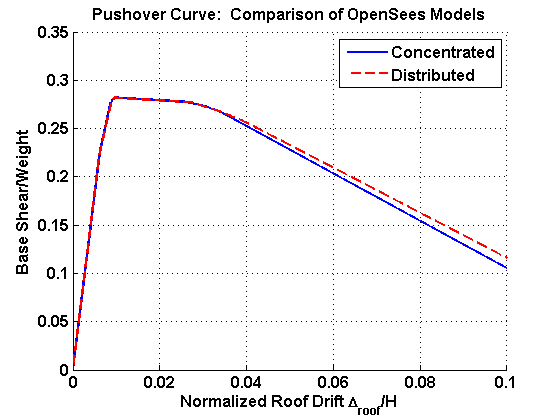
Theoretically, the results of the distributed plasticity model should approach those of the concentrated plasticity model as the length of the plastic hinge regions approaches zero. Because of localized instability due to the stress-strain formulation of the beam with hinges element, the distributed plasticity model does not give reasonable results when the length of the plastic hinge is very small (i.e., 10e-5). Therefore, the length of the plastic hinges was increased from 10e-5 until the results of this model approached those of the concentrated plasticity model. The plastic hinge length that led to agreement between the models was 0.4% of the frame member's total length. The periods of the concentrated and distributed models are very close: T1 = 0.83 s (con) vs. 0.82 s (dist) and T2 = 0.22 s (con) vs. 0.21 s (dist).
The results of the pushover analyses from the OpenSees models are shown in Figure 3. This figure shows the normalized base shear (base shear divided by the weight of the structure) versus the roof drift (roof displacement divided by the roof elevation). The models are nearly identical until about 2.5% roof drift when their curves begin to diverge. The descending branch of the the concentrated plasticity model is slightly steeper, but the two models agree reasonably well as there is less than 10% percent difference in the base shears at 10% roof drift.
Comparison of OpenSees & SAP2000 Results
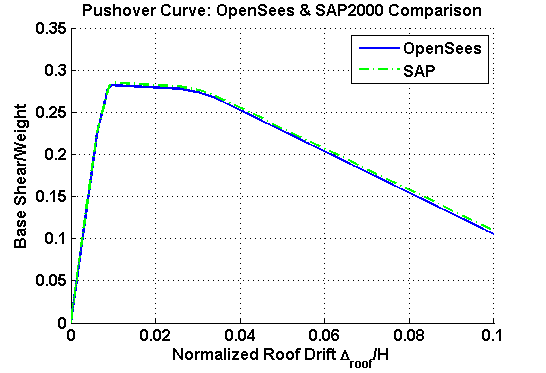
The results of the pushover analyses from the concentrated plasticity OpenSees model and the SAP2000 model are shown in Figure 4.The OpenSees and SAP2000 models agree very well as the difference between their base shears at 10% roof drift is only 4%.
References
- Ibarra, L. F., and Krawinkler, H. (2005). “Global collapse of frame structures under seismic excitations,” Technical Report 152, The John A. Blume Earthquake Engineering Research Center, Department of Civil Engineering, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports]
- Ibarra, L. F., Medina, R. A., and Krawinkler, H. (2005). “Hysteretic models that incorporate strength and stiffness deterioration,” Earthquake Engineering and Structural Dynamics, Vol. 34, 12, pp. 1489-1511.
- Lignos, D. G., and Krawinkler, H. (2012). “Sidesway Collapse of Deteriorating Structural Systems under Seismic Excitations,” Technical Report 177, The John A. Blume Earthquake Engineering Research Center, Department of Civil Engineering, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports]
- Lignos, D. G., and Krawinkler, H. (2011). “Deterioration Modeling of Steel Beams and Columns in Support to Collapse Prediction of Steel Moment Frames,” ASCE, Journal of Structural Engineering, Vol. 137 (11), 1291-1302.