ElastomericX

This command is used to construct an ElastomericX bearing element object in three-dimension. The 3D continuum geometry of an elastomeric bearing is modeled as a 2-node, 12 DOF discrete element. This elements extends the formulation of Elastomeric_Bearing_(Bouc-Wen)_Element element. However, instead of the user providing material models as input arguments, it only requires geometric and material properties of an elastomeric bearing as arguments. The material models in six direction are formulated within the element from input arguments. The time-dependent values of mechanical properties (e.g., shear stiffness, buckling load capacity) can also be recorded using the "parameters" recorder.

For a 3D problem:

element ElastomericX $eleTag $Nd1 $Nd2 $Fy $alpha $Gr $Kbulk $D1 $D2 $ts $tr $n <<$x1 $x2 $x3> $y1 $y2 $y3> <$kc> <$PhiM> <$ac> <$sDratio> <$m> <$cd> <$tc> <$tag1> <$tag2> <$tag3> <$tag4>

---

$eleTag	unique element object tag
$Nd1 $Nd2	end nodes
$Fy	yield strength
$alpha	post-yield stiffness ratio
$Gr	shear modulus of elastomeric bearing
$Kbulk	bulk modulus of rubber
$D1	internal diameter
$D2	outer diameter (excluding cover thickness)
$ts	single steel shim layer thickness
$tr	single rubber layer thickness
$n	number of rubber layers
$x1 $x2 $x3	vector components in global coordinates defining local x-axis (optional)
$y1 $y2 $y3	vector components in global coordinates defining local y-axis (optional)
$kc	cavitation parameter (optional, default = 10.0)
$PhiM	damage parameter (optional, default = 0.5)
$ac	strength reduction parameter (optional, default = 1.0)
$sDratio	shear distance from iNode as a fraction of the element length (optional, default = 0.5)
$m	element mass (optional, default = 0.0)
$cd	viscous damping parameter (optional, default = 0.0)
$tc	cover thickness (optional, default = 0.0)
$tag1	Tag to include cavitation and post-cavitation (optional, default = 0)
$tag2	Tag to include buckling load variation (optional, default = 0)
$tag3	Tag to include horizontal stiffness variation (optional, default = 0)
$tag4	Tag to include vertical stiffness variation (optional, default = 0)

Important note:

Because default values of heating parameters are in SI units, user must override the default heating parameters values if using Imperial units
User should distinguish between yield strength of elastomeric bearing (Fy) and characteristic strength (Qd): Qd=Fy*(1-alpha)

Physical Model and Mechanical Properties

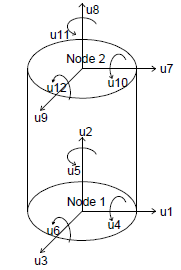
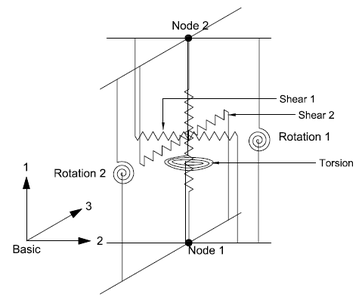
The physical model of an elastomeric bearing is considered as a two-node, twelve degrees-of-freedom discrete element. The two nodes are connected by six springs that represent the mechanical behavior in the six basic directions of a bearing. The degrees of freedom and discrete spring representation of an elastomeric bearing is shown in the below figures.

The general form of element force vector, <math>{{f}_{b}}</math>, and element stiffness matrix,<math>{{K}_{b}}</math> , for element representation considered above is given by equation below:

<math>{{f}_{b}}=\left[ \begin{matrix}

  Axial  \\
  Shear1  \\
  Shear2  \\
  Torsion  \\
  Rotation1  \\
  Rotation2  \\

\end{matrix} \right];\ \ \ \ \ \ {{K}_{b}}=\left[ \begin{matrix}

  Axial & 0 & 0 & 0 & 0 & 0  \\
  0 & Shear1 & Shear12 & 0 & 0 & 0  \\
  0 & Shear21 & Shear2 & 0 & 0 & 0  \\
  0 & 0 & 0 & Torsion & 0 & 0  \\
  0 & 0 & 0 & 0 & Rotation1 & 0  \\
  0 & 0 & 0 & 0 & 0 & Rotation2  \\

\end{matrix} \right]</math>

The coupling of the two shear springs is considered directly by using a coupled bidirectional model. All other springs are uncoupled. The coupling of vertical and horizontal directions are considered indirectly by using expressions for mechanical properties in one direction that are dependent on the response parameters in the other direction. Linear uncoupled springs are considered in the torsion and the two rotational springs as they are not expected to significantly affect the response of an elastomeric bearing. The off-diagonal terms due to coupling between axial and shear, and axial and rotation, are not considered in the two-spring model (Koh and Kelly, 1987) used here. An exact model would have non-zero values of these off-diagonal terms. A discussion on the formulation of the two-spring model and the exact model is presented in Ryan et al.(1991). The subscript b refers to the element’s basic coordinate system. The response quantities are transformed between the basic, local and global coordinates to perform computations.

The discrete spring model presented here has the advantages of easy implementation and being computationally efficient. The mechanical properties of the six springs (also referred to as material models in OpenSees) are defined using analytical solutions available from the analysis of elastomeric bearings. The expression for mechanical properties, including stiffness and buckling load capacity, are derived using explicit consideration for geometric nonlinearity due to large displacement effects. The material models in six directions are:

• Axial direction: a new mathematical model that captures the behavior under cyclic tension Link
• Two shear directions: a special case of the Bouc-Wen model extended by Nagarajaiah et al.(1991) for seismic isolation bearings
• Torsion: a linear elastic model
• Two rotational directions: linear elastic models

In addition to the behavior captured by existing bearing elements, this element can capture following characteristics:

1. Cavitation and post-cavitation behavior in tension (tag1)
2. Variation in critical buckling load capacity due to lateral displacement (tag2)
3. Variation in horizontal shear stiffness with axial load on the bearing (tag3)
4. Variation in vertical axial stiffness with horizontal displacement (tag4)

User may choose to include an individual or a combination of these behaviors through user tags (include:1, exclude:0) in their analysis.

For the full capabilities of this element, users are referred to: EESD Article

Consideration of characteristics to include under extreme loading

A recent paper by Kumar et. al (2015) explains which of the four tags should be included in the analysis. Although the analysis presented in the paper is for the base-isolated NPP, the conclusions are valid for design earthquake and maximum considered earthquake for regular building structures as well. Following are few thumb rules that can be followed: tag 1: Unless you are investigating the tensile behavior, the effect of the tensile model on shear response is insignificant. tag 2: It is recommended to use tag to include variable buckling load capacity. It affects the compression capacity and shear stiffness. The apparent softening in shear force-deformation behavior at high axial load is due to this. A constant buckling load will show less softening. tag 3: Recommended if axial load expected during the loading is more than 10% of the buckling load capacity. tag2+tag3 provide greater softening. tag 4: Unless you are investigating the axial behavior, the effect of the tensile model on shear response is insignificant.

Verification and validation

This is element has been verified per ASME guidelines. Users are referred to the SMiRT23 Paper and chapter 4 of the Manish Kumar's Dissertation for complete details.

Recorders

In addition to regular recorders provided by the bearing elements ( Element Recorder), this element can also record instantaneous values of cavitation force (Fcn), buckling load capacity (Fcrn), vertical stiffness (Kv) and horizontal stiffness (ke) using the "Parameters" recorder in that order.

        Example: recorder Element <-file $fileName> -time <-ele ($ele1 $ele2 ...)> Parameters
        recorder Element -file param.out -time -ele 1 Parameters

To check if bearing has buckled or cavitated, an user can obtain the histories of Fcn and Fcrn as described above and divide the axial force (obtained from basicForce recorder, qb(2)) by Fcn and Fcrn at each time step, which provides demand vs capacity (D/C) ratios at each time step. If Fcn/qb(0) > 1.0 : Cavitation, or Fcrn/qb(0)>1.0 : Buckling.

Examples

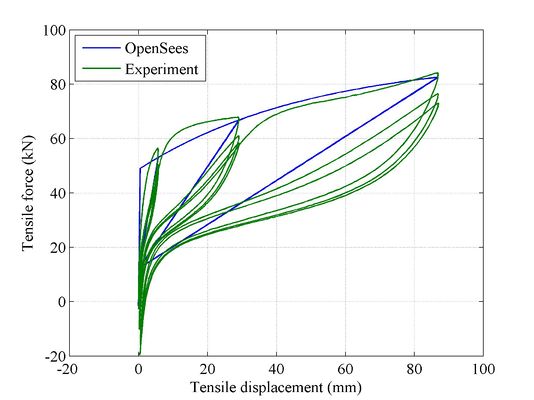
An example is presented here in which a low damping rubber bearing (LDR 5 in Warn(2006)) is subjected to a tensile harmonic loading in laboratory (SEESL at UB). The response obtained from ElastomericX element in OpenSees is compared with the experimental results. The behavior of elastomeric bearing in shear and compression is well established, and is not explored here.

element ElastomericX 1 1 2 $Fy_h $alpha $G $K $D1 $D2 $ts $tr $n 0 1 0 1 0 0 $kc $PhiM $ac 0.5 0.0 $cd $tc 1 0 0 0

Excitation files: File:Excitation Warn.zip ‎

Tcl files: File:EBgravity.tcl File:EBtest.tcl

More examples of this element would be uploaded soon!

References

1. Kumar, M., Whittaker, A., and Constantinou, M. (2014). "An advanced numerical model of elastomeric seismic isolation bearings." Earthquake Engineering & Structural Dynamics, 43(13), 1955-1974. Link
2. Kumar, M., Whittaker, A., and Constantinou, M. (2015). "Experimental investigation of cavitation in elastomeric seismic isolation bearings." Engineering Structures, 101, 290-305. Link
3. Kumar, M., Whittaker, A., and Constantinou, M. (2015). "Response of base-isolated nuclear structures to extreme earthquake shaking." Nuclear Engineering and Design (In press). Link
4. Warn, G. P. (2006). "The coupled horizontal-vertical response of elastomeric and lead-rubber seismic isolation bearings." PhD Dissertation, Civil, Structural and Environmental Engineering, University at Buffalo.
5. Koh, C. G., and Kelly, J. M. (1987). "Effects of axial load on elastomeric isolation bearings." EERC/UBC 86/12, Earthquake Engineering Research Center, University of California, Berkeley, United States, 108p.
6. Nagarajaiah, S., Reinhorn, A. M., and Constantinou, M. C. (1991). "Nonlinear dynamic analysis of 3-d-base-isolated structures." Journal of structural engineering New York, N.Y., 117(7), 2035-2054.
7. Ryan, K. L., Kelly, J. M., and Chopra, A. K. (2005). "Nonlinear model for lead-rubber bearings including axial-load effects." Journal of Engineering Mechanics, 131(12), 1270-1278.

---

Code Developed by: Manish Kumar, University at Buffalo, SUNY.

Any bugs in this element can be reported to mkumar2 AT buffalo dot edu