CFSWSWP
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a uniaxialMaterial model that simulates the hysteresis response (Shear strength-Lateral displacement) of a wood-sheathed cold-formed steel shear wall panel (CFS-SWP). The hysteresis model has smooth curves and takes into account the strength and stiffness degradation, as well as pinching effect.
This uniaxialMaterial gives results in Newton and Meter units, for strength and displacement, respectively.
NOTE: before you use this material make sure that you have downloaded the latest OpenSees version.
| uniaxialMaterial CFSWSWP $tag $height $width $fut $tf $Ife $Ifi $ts $np $ds $Vs $sc $nc $type $openingArea $openingLength |
| $matTag | Integer identifier used to tag the material model |
| $height | SWP’s height (mm) |
| $width | SWP’s width (mm) |
| $fuf | Tensile strength of framing members (MPa) |
| $tf | Framing thickness (mm) |
| $Ife | Moment of inertia of the double end-stud (mm4) |
| $Ifi | Moment of inertia of the intermediate stud (mm4) |
| $ts | Sheathing thickness (mm) |
| $np | Sheathing number (one or two sides sheathed) |
| $ds | Screws diameter (mm) |
| $Vs | Screws shear strength (N) |
| $sc | Screw spacing on the SWP perimeter (mm) |
| $nc | Total number of screws located on the SWP perimeter |
| $type | Integer identifier used to define wood sheathing type (DFP=1, OSB=2, CSP=3) |
| $openingArea | Total area of openings (mm²) |
| $openingLength | Cumulative length of openings (mm) |
DESCRIPTION:
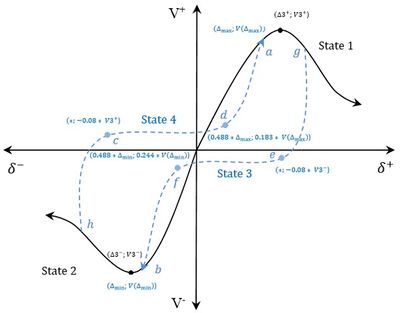
The uniaxial hysteresis model of Cold-Formed Steel Shear Wall Panel (CFS-SWP) consists of three parts: backbone curves of the hysteresis loops (states 1 and 2), hysteresis criteria (unloading-reloading path: states 3 and 4) (Fig.2) and deterioration criteria. The following paragraphs will respectively introduce the terms of the three parts.
Maximum lateral shear strength and the associated displacement are assessed using an analytical method for wood sheathed CFS SWP proposed by Xu L and Martinez J (2007) which takes into account a wide range of factors that affect the behaviour and strength of a CFS SWP, namely: material properties, thickness and geometry of sheathing and framing, spacing of studs, construction details such as size and spacing of sheathing-to-framing connections.
In addition to the envelope curve, the proposed hysteresis model requires the introduction of parameters that define the strength and stiffness deterioration, as well as the pinching effect under cyclic loading. Compared to the monotonic test result, the hysteresis response of CFS SWP exhibits strength deterioration; even if the displacement associated to peak strength has not been reached yet. The stiffness deterioration of the proposed model is positively related to strength degraded degree, and is defined in a same way as the strength deterioration.
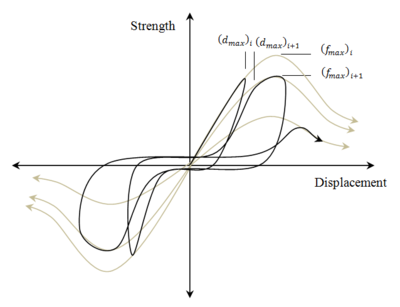
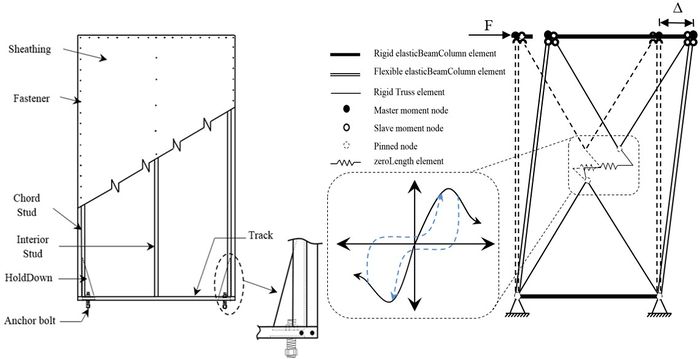
In order to account for the overall lateral stiffness and strength of the SWP, an equivalent simple non-linear zeroLength element connected to rigid truss elements which transmit the force to the boundary studs that resist the uniaxial tension and compression stress is used (Fig.3). This modeling tip leads to a considerable reduction in terms of elements number constituting the CFS SWP. The boundary members form a mechanism and the lateral stiffness and strength are derived directly from the zeroLength element. The CFS SWP details, as well as a schematic representation of the finite element model are illustrated in Fig.3.
EXAMPLES:
Cold-Formed Steel Wood Sheathed Shear Wall Panel examples
REFERENCES:
Smail Kechidi, Hysteresis model development for cold-formed steel shear wall panel based on physical and mechanical characteristics, Master Thesis, University of Blida 1, Algeria, 2014.
Smail Kechidi and Nouredine Bourahla, Deteriorating hysteresis model for cold-formed steel shear wall panel based on physical and mechanical characteristics, OpenSees Days Portugal 2014- Workshop on Multi-Hazard Analysis of Structures using OpenSees, Porto 3-4, Portugal, July 2014.
L.N. Lowes, A. Altoontash, Modelling reinforced-concrete beam-column joints subjected to cyclic loading, Journal of Structural Engineering, 129(12):1686-1697, 2003.
A.E. Branston, Y.C. Chen, F.A. Boudreault and C.A. Rogers, Testing of light-gauge steel frame wood structural panel shear walls, Canadian Journal of Civil Engineering, 33(9):561-572, 2006.
J. Martinez and L. Xu, Strength and stiffness determination of shear wall panels in cold-formed steel framing, Thin-Walled Structures, 44(10):1084-1095, 2006.
Code Developed by: Smail Kechidi and Nouredine Bourahla, University of Blida 1, Algeria
Images Developed by: Smail Kechidi, University of Blida 1, Algeria
Authors contact:
Smail Kechidi, PhD student at University of Blida 1, Algeria, s_kechidi@univ-blida.dz, smail.kechidi@gmail.com
Nouredine Bourahla, Professor at University of Blida 1, Algeria, nbourahla@univ-blida.dz