Contact Author: |
Michael H. Scott Oregon State University http://web.engr.oregonstate.edu/~mhscott/
|
|
Reference: |
Scott, M.H. and G.L. Fenves. "Plastic Hinge Integration Methods for Force-Based Beam-Column Elements", Journal of Structural Engineering, ASCE, 132(2):244-252, February 2006. |
|
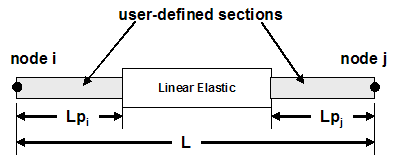
This command is used to construct a beamWithHinges element object, which is based on the non-iterative (or iterative) flexibility formulation, and considers plasticity to be concentrated over specified hinge lengths at the element ends.
Note, the beamWithHinges element localize plastic hinging at the element ends only.
This type of element divides the element in three parts: two hinges at the ends, and a linear-eleastic region in the middle. The hinges are defined by assigning to each a previously-defined section. The length of the each hinge is also specified by the user:
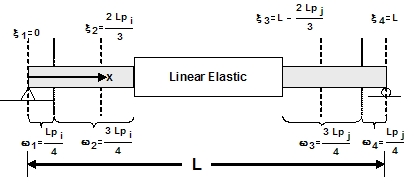
While the integration of distributed-plasticity force-base elements distributes the gauss points along the entire element length, the beamWithHinges element localizes the integration points in the hinge regions. Two integration points per hinge are used to be able represent the curvature distribution accurately -- Gauss-Radau Integration:
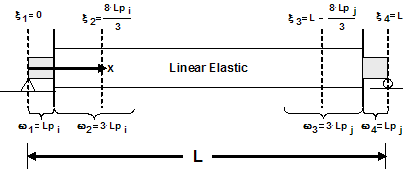
Two integration points per hinge, however, require too much computational overhead. A Modified Gauss-Radau Integration, developed by Scott et al., would apply the Gauss-Radau hinge integration over 4Lp instead of Lp. Elastic properties are then applied to the interior integration points, where a closed-form solution is used:
There are many advantages to this formulation over the other types of beamWithHinges:
The arguments for the construction of the element depend on the dimension of the problem, ndm.
For a two-dimensional problem:
element beamWithHinges $eleTag $iNode $jNode $secTagI $Lpi $secTagJ $Lpj $E $A $Iz $transfTag <-mass $massDens> <-iter $maxIters $tol>
For a three-dimensional problem:
element beamWithHinges $eleTag $iNode $jNode $secTagI $Lpi $secTagJ $Lpj $E $A $Iz $Iy $G $J $transfTag <-mass $massDens> <-iter $maxIters $tol>
$eleTag |
unique element object tag |
|
$iNode |
$jNode |
end nodes |
$secTagI |
identifier for previously-defined section object corresponding to node i |
|
$Lpi |
hinge length at node i |
|
$secTagJ |
identifier for previously-defined section object corresponding to node j |
|
$Lpj |
hinge length at node j |
|
$E |
Young's Modulus |
|
$A |
area of element cross-section |
|
$Iz |
section moment of inertia about the section local z-axis |
|
$Iy |
section moment of inertia about the section local y-axis |
|
$G |
Shear Modulus |
|
$J |
torsional moment of inertia of cross section |
|
$transfTag |
identifier for previously-defined coordinate-transformation (CrdTransf) object |
|
$massDens |
element mass density (per unit length), from which a lumped-mass matrix is formed (optional, default=0.0) |
|
$maxIters |
maximum number of iterations to undertake to satisfy element compatibility (optional, default=1) |
|
$tol |
tolerance for satisfaction of element compatibility (optional, default=10-16) |
|
The -iter switch enables the iterative form of the flexibility formulation. Note that the iterative form can improve the rate of global convergence at the expense of more local element computation.
NOTE: The elastic properties are integrated only over the beam interior, which is considered to be linear-elastic.
The valid queries to a beamWithHinges element when creating an ElementRecorder object are 'force,' 'stiffness,' 'rotation' (hinge rotation), or 'section $secNum secArg1 secArg2...' Where $secNum refers to the integration point whose data is to be output.
NOTE: The beamWithHinges element used here has four elastic sections and two fiber section at the end. Therefore for output in specifying $secNum:
$secNum=1: hinge at node i
$secNum=6: hinge at node j