constraints Command

This command is used to construct the ConstraintHandler object. The ConstraintHandler object determines how the constraint equations are enforced in the analysis. Constraint equations enforce a specified value for a DOF, or a relationship between DOFs. The degrees of freedom can be broken down into U_R, the retained DOF's, and U_C, the condensed DOF's:

• The Plain Constraints command is used to enforce homogeneous single-point constraints, such as the case of homogeneous boundary conditions, where all boundary conditions are fixity, using single-point constraints (Single-Point Constraints, http://www.). For this case: U_C=0.0

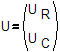
The other constraints commands are used for ALL other cases, such as the case of non-homogeneous single-point constraints using the sp command, multi-point constraints, imposed motions and multi-support excitation. For such cases, the relationship between DOF's can be written as:U_C=C_RCU_R. Where C_RC is a matrix of constants.

The following constraints handlers are currently availble:

• Penalty Method -- consists of adding large numbers to the stiffness matrix and the restoring-force vectors to impose a prescribed zero or nonzero DOF. This method applies very stiff elements (numerically) at the boundary conditions. These additional stiffnesses affect the eigenvalues/eigenvectors in a transient analysis. This is the recommended method for a static analysis.
• Lagrange Multipliers -- apply the method of lagrange multipliers to the system of equations, thus enlarging the size of the materices. Once Labrange Multipliers have been applied, the resulting stiffness matrix is no longer positive definite. Therefore, this method should be used only if there are condition-number problems with the penalty method.
• Transformation Method -- transforms the stiffness matrix by condensing out the constrained DOF's. This method reduces the size of the system for multi-point constraints. This is the recommended method for a transient analysis. However, this method should not be used when nodes are constrained in series. For example, U₃ is constrained to U₂, which is then constrained to U₁.

Of the different methods, "the Lagrange multiplier method is more attractive than the transformation method if there are few constraint equations that couple many DOF. However, Lagrange multipliers are active at the structure level, but transformation equations can be applied at either the structure level or element by element. The latter has the appeal of disposing of constraints at an early stage, when the matrices are small and manageable". (Cook)

"In comparison with Lagrange multipliers, penalty functions have the advantage of introducing no new variables. However, the penalty matrix may significantly increase the bandwidth of the structural equations, depending on how DOF are numbered and what DOF are coupled by the constraint equations. Penalty functions have the disadvantage that penalty numbers must be chosen in an allowable range: large enough to be effective but not so large as to provoke numerical difficulties". (Cook)

More information and examples on these methods are discussed in detail in the Cook book.