Contact Author: |
Davide Fugazza: davide.fugazza@tiscali.it |
This command is used to construct a uniaxial superelastic shape-memory alloy material model. The material behavior is assumed to be symmetric, therefore the material response in traction is the same as that in compression. The model requires 6 material parameters.
uniaxialMaterial SMA $matTag $E $eps_L $sig_AM_s $sig_AM_f $sig_MA_s $sig_MA_f
$matTag |
unique material object integer tag |
$E |
Young's modulus of austenite and martensite |
$eps_L |
plateau length |
$sig_AM_s |
stress level at which austenite-to-martensite phase transformation starts |
$sig_AM_f |
stress level at which austenite-to-martensite phase transformation finishes |
$sig_MA_s |
stress level at which martensite-to-austenite phase transformation starts |
$sig_MA_f |
stress level at which martensite-to-austenite phase transformation finishes |
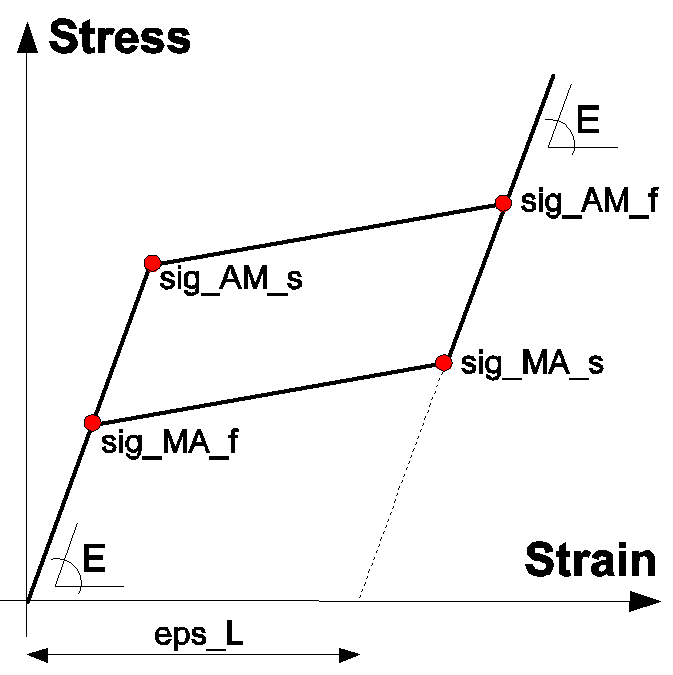
Figure 1: stress-strain relationship exhibited by the superelastic shape-memory alloy constitutive model. Sketch of the material response under tensile loads.
Model Characteristic:
Such a model (Fugazza, 2003), which is a modification of the one proposed by Auricchio and Sacco (1997), is capable of describing the material behavior under arbitrary loadings, such as those involved in seismic excitations, where the response is mainly composed by sub-hysteresis loops internal to the main one associated with complete phase transformations. The model formulation, developed in the small deformation regime, relies on the assumption that the relationship between stresses and strains is represented by a series of straight lines whose form is determined by the extent of the transformation experienced. Further assumptions made are that no strength degradation occurs during cycling and that austenite and martensite branches have the same modulus of elasticity.
It is assumed to work with one scalar internal variable, csi, representing the martensite fraction and with two processes which may produce its variation:
For both processes, linear kinetic rules to describe the evolution in time of the martensite fraction are chosen. In particular, the activation conditions for the conversion of austenite into martensite are:
Sig_AM_s < |sig| < sig_AM_f and d |sig| / dt >0
where sig_AM_s and sig_AM_f are material parameters representing the stress levels at which the A ----> M transformation starts and finishes respectively. The corresponding evolutionary equation is set equal to:
d(csi) / dt = -(1 – csi ) [d |sig| / dt ] / [ |sig| - sig_AM_f ]
On the other hand, the activation conditions for the conversion of martensite into austenite are:
sig_MA_f < |sig| <sig_MA_s and d |sig| /dt <0
where sig_MA_f and sig_MA_s are material parameters representing the stress levels at which the M -----> A transformation starts and finishes respectively. The corresponding evolutionary equation is set equal to:
d(csi) / dt = cis [d |sig| / dt] / [ |sig| - sig_MA_f ]
Limiting the discussion to a small deformation regime, the following additive decomposition of the total strain, eps, is assumed:
eps = eps_el + eps_L * csi * sgn(sig)
where eps_el is the elastic strain, eps_L is the maximum residual strain and sgn(?) is the sign function. Finally, the elastic strain is assumed to be linearly related to the stress:
sig = E*esp_el
with E the elastic modulus of both the austenitic and martensitic branch.
References:
Auricchio, F., Sacco, E. (1997). "A one-dimensional model for superelastic shape-memory alloys with different elastic properties between austenite and martensite", International Journal of Non-Linear Mechanics, 32, 1101-1114.
Fugazza, D. (2003). "Shape-memory alloy devices in earthquake engineering: mechanical properties, constitutive modelling and numerical simulations", Master's thesis, European School for Advanced Studies in Reduction of Seismic Risk (ROSE School), Pavia, Italy.