In this next example the use of variable substitution and the Tcl loop control structure for building models is demonstrated.
This example is of a reinforced concrete multibay two story frame, as shown in the figure, subject to gravity loads.
Files Required
Model
A model of the frame shown in the figure is created. The number of objects in the model is dependent on the parameter numBay. The $($ numBay $+1)*3)$ nodes are created, one column line at a time, with the node at the base of the columns fixed in all directions. Three materials are constructed, one for the concrete core, one for the concrete cover and one for the reinforcement steel. Three fiber discretized sections are then built, one for the exterior columns, one for the interior columns and one for the girders. Each of the members in the frame is modelled using nonlinear beam-column elements with 4 (nP) integration points and a linear geometric transformation object.
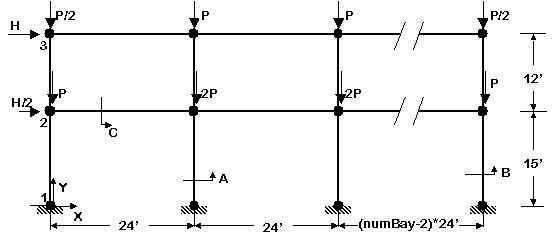
For gravity loads, a single load pattern with a linear time series and two vertical nodal loads acting at the first and second floor nodes of each column line is used. The load at the lower level is twice that of the upper level and the load on the interior columns is twice that of the exterior columns.
For the lateral load analysis, a second load pattern with a linear time series is introduced after the gravity load analysis. Associated with this load pattern are two nodal loads acting on nodes 2 and 3, with the load level at node 3 twice that acting at node 2.
Analysis
A solution Algorithm of type Newton is created. The solution algorithm uses a ConvergenceTest based on the norm of the displacement increment vector. The integrator for the analysis will be LoadControl with a load step increment of 0.1. The storage for the system of equations is BandGeneral. The equations are numbered using an RCM (reverse Cuthill-McKee) numberer. The constraints are enforced with a Plain constraint handler. Once the components of the analysis have been defined, the analysis object is then created. For this problem a Static analysis object is used and 10 steps are performed to load the model with the desired gravity load.
After the gravity load analysis has been performed, the gravity loads are set to constant and the time in the domain is reset to 0.0. A new LoadControl integrator is now added. The new LoadControl integrator has an initial load step of 1.0, but this can vary between 0.02 and 2.0 depending on the number of iterations required to achieve convergence at each load step. 100 steps are then performed.
Output Specification
For the pushover analysis the lateral displacements at nodes 2 and 3 will be stored in the file Node41.out for post-processing. In addition, if the variable displayMode is set to ``displayON'' the load-displacement curve for horizontal displacements at node 3 will be displayed in a window on the user's terminal.
OpenSees Script
# OpenSees Example 4.1
# OpenSees Primer
#
# Units: kips, in, sec
# Parameter identifying the number of bays
set numBay 3
# ------------------------------
# Start of model generation
# ------------------------------
# Create ModelBuilder (with two-dimensions and 3 DOF/node)
model BasicBuilder -ndm 2 -ndf 3
# Create nodes
# ------------
# Set parameters for overall model geometry
set bayWidth 288
set nodeID 1
# Define nodes
for {set i 0} {$i <= $numBay} {incr i 1} {
set xDim [expr $i * $bayWidth]
# tag X Y
node $nodeID $xDim 0
node [expr $nodeID+1] $xDim 180
node [expr $nodeID+2] $xDim 324
incr nodeID 3
}
# Fix supports at base of columns
for {set i 0} {$i <= $numBay} {incr i 1} {
# node DX DY RZ
fix [expr $i*3+1] 1 1 1
}
# Define materials for nonlinear columns
# ------------------------------------------
# CONCRETE
# Cover concrete
# tag -f'c -epsco -f'cu -epscu
uniaxialMaterial Concrete01 1 -4.00 -0.002 0.0 -0.006
# Core concrete
uniaxialMaterial Concrete01 2 -5.20 -0.005 -4.70 -0.02
# STEEL
# Reinforcing steel
# tag fy E0 b
uniaxialMaterial Steel01 3 60 30000 0.02
# Define cross-section for nonlinear columns
# ------------------------------------------
# Interior column section - Section A
section Fiber 1 {
# mat nfIJ nfJK yI zI yJ zJ yK zK yL zL
patch quadr 2 1 12 -11.5 10 -11.5 -10 11.5 -10 11.5 10
patch quadr 1 1 14 -13.5 -10 -13.5 -12 13.5 -12 13.5 -10
patch quadr 1 1 14 -13.5 12 -13.5 10 13.5 10 13.5 12
patch quadr 1 1 2 -13.5 10 -13.5 -10 -11.5 -10 -11.5 10
patch quadr 1 1 2 11.5 10 11.5 -10 13.5 -10 13.5 10
# mat nBars area yI zI yF zF
layer straight 3 6 1.56 -10.5 9 -10.5 -9
layer straight 3 6 1.56 10.5 9 10.5 -9
}
# Exterior column section - Section B
section Fiber 2 {
patch quadr 2 1 10 -10 10 -10 -10 10 -10 10 10
patch quadr 1 1 12 -12 -10 -12 -12 12 -12 12 -10
patch quadr 1 1 12 -12 12 -12 10 12 10 12 12
patch quadr 1 1 2 -12 10 -12 -10 -10 -10 -10 10
patch quadr 1 1 2 10 10 10 -10 12 -10 12 10
layer straight 3 6 0.79 -9 9 -9 -9
layer straight 3 6 0.79 9 9 9 -9
}
# Girder section - Section C
section Fiber 3 {
patch quadr 1 1 12 -12 9 -12 -9 12 -9 12 9
layer straight 3 4 1.00 -9 9 -9 -9
layer straight 3 4 1.00 9 9 9 -9
}
# Define column elements
# ----------------------
# Number of integration points
set nP 4
# Geometric transformation
geomTransf Linear 1
set beamID 1
# Define elements
for {set i 0} {$i <= $numBay} {incr i 1} {
# set some parameters
set iNode [expr $i*3 + 1]
set jNode [expr $i*3 + 2]
for {set j 1} {$j < 3} {incr j 1} {
# add the column element (secId == 2 if external, 1 if internal column)
if {$i == 0} {
element nonlinearBeamColumn $beamID $iNode $jNode $nP 2 1
} elseif {$i == $numBay} {
element nonlinearBeamColumn $beamID $iNode $jNode $nP 2 1
} else {
element nonlinearBeamColumn $beamID $iNode $jNode $nP 1 1
}
# increment the parameters
incr iNode 1
incr jNode 1
incr beamID 1
}
}
# Define beam elements
# ----------------------
# Number of integration points
set nP 4
# Geometric transformation
geomTransf Linear 2
# Define elements
for {set j 1} {$j < 3} {incr j 1} {
# set some parameters
set iNode [expr $j + 1]
set jNode [expr $iNode + 3]
for {set i 1} {$i <= $numBay} {incr i 1} {
element nonlinearBeamColumn $beamID $iNode $jNode $nP 3 2
# increment the parameters
incr iNode 3
incr jNode 3
incr beamID 1
}
}
# Define gravity loads
# --------------------
# Constant gravity load
set P -192
# Create a Plain load pattern with a Linear TimeSeries
pattern Plain 1 Linear {
# Create nodal loads at nodes
for {set i 0} {$i <= $numBay} {incr i 1} {
# set some parameters
set node1 [expr $i*3 + 2]
set node2 [expr $node1 + 1]
if {$i == 0} {
load $node1 0.0 $P 0.0
load $node2 0.0 [expr $P/2.0] 0.0
} elseif {$i == $numBay} {
load $node1 0.0 $P 0.0
load $node2 0.0 [expr $P/2.0] 0.0
} else {
load $node1 0.0 [expr 2.0*$P] 0.0
load $node2 0.0 $P 0.0
}
}
}
# ------------------------------
# End of model generation
# ------------------------------
# ------------------------------------------------
# Start of analysis generation for gravity analysis
# -------------------------------------------------
# Create the convergence test, the norm of the residual with a tolerance of
# 1e-12 and a max number of iterations of 10
test NormDispIncr 1.0e-8 10 0
# Create the solution algorithm, a Newton-Raphson algorithm
algorithm Newton
# Create the integration scheme, the LoadControl scheme using steps of 0.1
integrator LoadControl 0.1 1 0.1 0.1
# Create the system of equation, a SPD using a profile storage scheme
system BandGeneral
# Create the DOF numberer, the reverse Cuthill-McKee algorithm
numberer RCM
# Create the constraint handler, the transformation method
constraints Plain
# Create the analysis object
analysis Static
# ------------------------------------------------
# End of analysis generation for gravity analysis
# -------------------------------------------------
# ------------------------------
# Perform gravity load analysis
# ------------------------------
# perform the gravity load analysis, requires 10 steps to reach the load level
analyze 10
# set gravity loads to be const and set pseudo time to be 0.0
# for start of lateral load analysis
loadConst -time 0.0
# ------------------------------
# Add lateral loads
# ------------------------------
# Reference lateral load for pushover analysis
set H 10
# Reference lateral loads
# Create a Plain load pattern with a Linear TimeSeries
pattern Plain 2 Linear {
load 2 [expr $H/2.0] 0.0 0.0
load 3 $H 0.0 0.0
}
# ------------------------------
# Start of recorder generation
# ------------------------------
# Create a recorder which writes to Node.out and prints
# the current load factor (pseudo-time) and dof 1 displacements at node 2 & 3
recorder Node -file Node41.out -time -node 2 3 -dof 1 disp
# Source in some commands to display the model
# comment out one of lines
set displayMode "displayON"
#set displayMode "displayOFF"
if {$displayMode == "displayON"} {
# a window to plot the nodal displacements versus load for node 3
recorder plot Node41.out Node_3_Xdisp 10 340 300 300 -columns 3 1 -dT 0.1
}
# ------------------------------
# End of recorder generation
# ------------------------------
# ------------------------------
# Start of lateral load analysis
# ------------------------------
# Change the integrator to take a min and max load increment
integrator LoadControl 1.0 4 0.02 2.0
# Perform the analysis
# Perform the pushover analysis
# Set some parameters
set maxU 10.0; # Max displacement
set controlDisp 0.0;
set ok 0;
while {$controlDisp < $maxU && $ok == 0} {
set ok [analyze 1]
set controlDisp [nodeDisp 3 1]
if {$ok != 0} {
puts "... trying an initial tangent iteration with Newton"
test NormDispIncr 1.0e-8 4000 0
algorithm ModifiedNewton -initial
set ok [analyze 1]
test NormDispIncr 1.0e-8 10 0
algorithm Newton
}
}
if {$ok != 0} {
puts "Pushover analysis FAILED"
} else {
puts "Pushover analysis completed SUCCESSFULLY"
}
Results
The output consists of the file Node41.out containing a line for each step of the lateral load analysis. Each line contains the load factor, the lateral displacements at nodes 2 and 3. A plot of the load-displacement curve for the frame is given in figure~\ref{twostory}.
FIGURE HERE