Modified Ibarra-Medina-Krawinkler Deterioration Model with Pinched Hysteretic Response (ModIMKPinching Material)
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
The original PinchingdMaterial material has been revised and should no longer be used. As the input format for the new material is slightly different, the old material will remain in the executable so that we do not break old scripts. However we will no longer document the command to use the old code. The new and improved material documentation is here:
The original command is included here for older users still wishing to use this material.
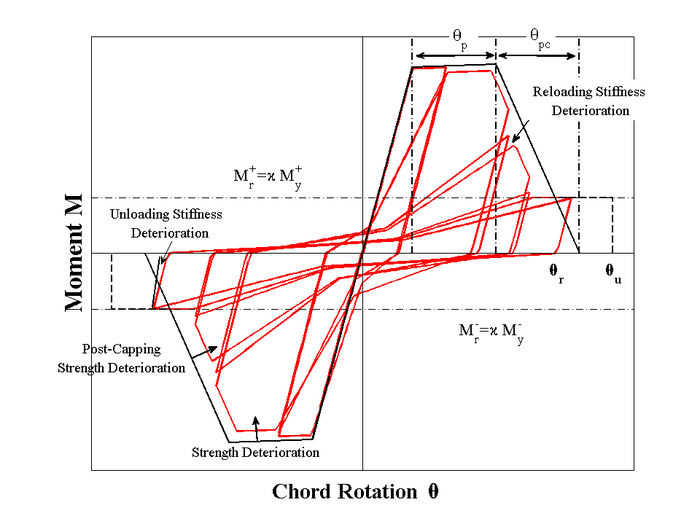
This command is used to construct a ModIMKPinching material. This material simulates the modified Ibarra-Medina-Krawinkler deterioration model with pinching hysteretic response. A youtube video presents a summary of this model including the way to be used within openSees (http://youtu.be/YHBHQ-xuybE).
| uniaxialMaterial ModIMKPinching $matTag $K0 $as_Plus $as_Neg $My_Plus $My_Neg $FprPos $FprNeg $A_pinch $Lamda_S $Lamda_C $Lamda_A $Lamda_K $c_S $c_C $c_A $c_K $theta_p_Plus $theta_p_Neg $theta_pc_Plus $theta_pc_Neg $Res_Pos $Res_Neg $theta_u_Plus $theta_u_Neg $D_Plus $D_Neg |
| $matTag | integer tag identifying material |
| $K0 | elastic stiffness |
| $as_Plus | strain hardening ratio for positive loading direction |
| $as_Neg | strain hardening ratio for negative loading direction |
| $My_Plus | effective yield strength for positive loading direction |
| $My_Neg | effective yield strength for negative loading direction (Must be defined as a negative value) |
| $FprPos | Ratio of the force at which reloading begins to force corresponding to the maximum historic deformation demand (positive loading direction) |
| $FprNeg | Ratio of the force at which reloading begins to force corresponding to the absolute maximum historic deformation demand (negative loading direction) |
| $A_Pinch | Ratio of reloading stiffness |
| $Lamda_S | Cyclic deterioration parameter for strength deterioration [E_t=Lamda_S*M_y, see Lignos and Krawinkler (2011); set Lamda_S = 0 to disable this mode of deterioration] |
| $Lamda_C | Cyclic deterioration parameter for post-capping strength deterioration [E_t=Lamda_C*M_y, see Lignos and Krawinkler (2011); set Lamda_C = 0 to disable this mode of deterioration] |
| $Lamda_A | Cyclic deterioration parameter for accelerated reloading stiffness deterioration [E_t=Lamda_A*M_y, see Lignos and Krawinkler (2011); set Lamda_A = 0 to disable this mode of deterioration] |
| $Lamda_K | Cyclic deterioration parameter for unloading stiffness deterioration [E_t=Lamda_K*M_y, see Lignos and Krawinkler (2011); set Lamda_K = 0 to disable this mode of deterioration] |
| $c_S | rate of strength deterioration. The default value is 1.0. |
| $c_C | rate of post-capping strength deterioration. The default value is 1.0. |
| $c_A | rate of accelerated reloading deterioration. The default value is 1.0. |
| $c_K | rate of unloading stiffness deterioration. The default value is 1.0. |
| $theta_p_Plus | pre-capping rotation for positive loading direction (often noted as plastic rotation capacity) |
| $theta_p_Neg | pre-capping rotation for negative loading direction (often noted as plastic rotation capacity) (must be defined as a positive value) |
| $theta_pc_Plus | post-capping rotation for positive loading direction |
| $theta_pc_Neg | post-capping rotation for negative loading direction (must be defined as a positive value) |
| $Res_Pos | residual strength ratio for positive loading direction |
| $Res_Neg | residual strength ratio for negative loading direction (must be defined as a positive value) |
| $theta_u_Plus | ultimate rotation capacity for positive loading direction |
| $theta_u_Neg | ultimate rotation capacity for negative loading direction (must be defined as a positive value) |
| $D_Plus | rate of cyclic deterioration in the positive loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0. |
| $D_Neg | rate of cyclic deterioration in the negative loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0. |
Image from: Lignos and Krawinkler (2012)
The deterioration model parameters can be calibrated based on actual experimental data of RC beams in terms of load - displacement or moment - rotation. Examples of such calibrations can be found in Lignos (2008) and Lignos and Krawinkler (2012).
References:
| [1] | Lignos, D.G., Krawinkler, H. (2012). “Development and Utilization of Structural Component Databases for Performance-Based Earthquake Engineering", Journal of Structural Engineering, ASCE, doi: 10.1061/(ASCE)ST.1943-541X.0000646. |
| [2] | Lignos, D.G., and Krawinkler, H. (2011). “Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading”, Journal of Structural Engineering, ASCE, Vol. 137 (11), 1291-1302. |
| [3] | Lignos, D.G. and Krawinkler, H. (2012). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Rep.No.TB 177, The John A. Blume Earthquake Engineering Research Center, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports] |
| [4] | Lignos, D.G. (2008). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Ph.D. Dissertation, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA. |
| [5] | Ibarra L.F., and Krawinkler, H. (2005). “Global collapse of frame structures under seismic excitations”, Rep. No. TB 152, The John A. Blume Earthquake Engineering Center, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports] |
| [6] | Ibarra L.F., Medina R. A., and Krawinkler H. (2005). “Hysteretic models that incorporate strength and stiffness deterioration”, Earthquake Engineering and Structural Dynamics, 34(12), 1489-1511. |
Code Developed by : by Dr. Dimitrios G. Lignos, McGill University