Eigen analysis of a two-storey shear frame
Example Provided by: Vesna Terzic, UC Berkeley
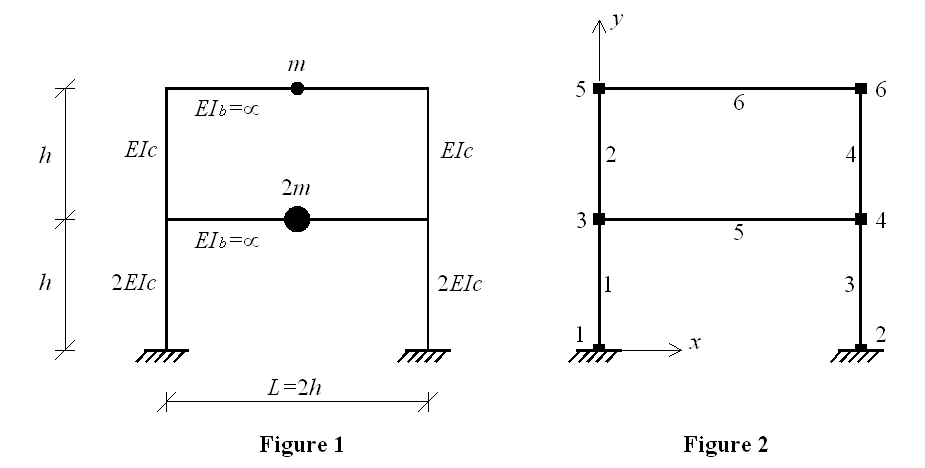
This example demonstrates how to perform eigenvalue analysis and plot mode shapes. Idealized two-storey shear frame (Example 10.4 from "Dynamic of Structures" book by Professor Anil K. Chopra) is used for this purpose. In this idealization beams are rigid in flexure, axial deformation of beams and columns are neglected, and the effect of axial force on the stiffness of the columns is neglected. Geometry and material characteristics of the frame structure are shown in Figure 1. Node and element numbering is given in Figure 2.
Instructions on how to run this example
To execute this ananlysis in OpenSees the user has to download this files:
Place EigenAnal_twoStoreyShearFrame.tcl in the same folder with the OpenSees.exe. By double clicking on OpenSees.exe the OpenSees interpreter will pop out. To run the analysis the user should type:
source EigenAnal_twoStoreyShearFrame8.tcl
and hit enter. To create output files (stored in directory "data") the user has to exit OpenSees interpreter by typing "exit".
Create the model
Spatial dimension of the model and number of degrees-of-freedom (DOF) at nodes are defined using model command. In this example we have 2D model with 3 DOFs at each node. This is defined in the following way:
model BasicBuilder -ndm 2 -ndf 3
Note: geometry, mass, and material characteristics are assigned to variables that correspond to the ones shown in Figure 1 (e.g., the height of the column is set to be 144 in. and assigned to variable h; the value of the height can be accessed by $h).
Nodes of the structure (Figure 2) are defined using the node command:
node 1 0. 0. ; node 2 $L 0. ; node 3 0. $h ; node 4 $L $h ; node 5 0. [expr 2*$h]; node 6 $L [expr 2*$h];
The boundary conditions are defined next using single-point constraint command fix. In this example nodes 1 and 2 are fully fixed at all three DOFs:
fix 1 1 1 1; fix 2 1 1 1;
Masses are assigned at nodes 3, 4, 5, and 6 using mass command. Since the considered shear frame system has only two degrees of freedom (displacements in x at the 1st and the 2nd storey), the masses have to be assigned in x direction only.
mass 3 $m 0. 0. ; mass 4 $m 0. 0. ; mass 5 [expr $m/2.] 0. 0. ; mass 6 [expr $m/2.] 0. 0. ;
The geometric transformation with id tag 1 is defined to be linear.
set TransfTag 1; geomTransf Linear $TransfTag ;
The beams and columns of the frame are defined to be elastic using elasticBeamColumn element. In order to make beams infinitely rigid moment of inertia for beams (Ib) is set to very high value (10e+12).
element elasticBeamColumn 1 1 3 $Ac $Ec [expr 2.*$Ic] $TransfTag; element elasticBeamColumn 2 3 5 $Ac $Ec $Ic $TransfTag; element elasticBeamColumn 3 2 4 $Ac $Ec [expr 2.*$Ic] $TransfTag; element elasticBeamColumn 4 4 6 $Ac $Ec $Ic $TransfTag; element elasticBeamColumn 5 3 4 $Ab $E $Ib $TransfTag; element elasticBeamColumn 6 5 6 $Ab $E $Ib $TransfTag;
To comply with the assumptions of the shear frame (no vertical displacemnts and rotations at nodes) end nodes of the beams are constrained to each other in the 2nd DOF (vertical displacement) and the 3rd DOF (rotation). EqualDOF command is used to imply these constraints.
equalDOF 3 4 2 3 equalDOF 5 6 2 3
Define recorders
For the specified number of eigenvalues (numModes) (for this example it is 2) the eigenvectors are recorded at all nodes in all DOFs using node recorder command.
for { set k 1 } { $k <= $numModes } { incr k } {
recorder Node -file [format "modes/mode%i.out" $k] -nodeRange 1 6 -dof 1 2 3 "eigen $k"
}
Perform eigenvalue analysis and store periods into a file
The eigenvalues are calculated using eigen commnad and stored in lambda variable.
set lambda [eigen $numModes];
The periods and frequencies of the structure are calculated next.
set omega {}
set f {}
set T {}
set pi 3.141593
foreach lam $lambda {
lappend omega [expr sqrt($lam)]
lappend f [expr sqrt($lam)/(2*$pi)]
lappend T [expr (2*$pi)/sqrt($lam)]
}
The periods are stored in a Periods.txt file inside of directory "modes".
set period "modes/Periods.txt"
set Periods [open $period "w"]
foreach t $T {
puts $Periods " $t"
}
close $Periods
Record the eigenvectors
For eigenvectors to be recorded record command has to be issued following the eigen command.
record
Display mode shapes
As there are two mode shapes of the system we will create two display windows using record display command. Here we specify window title (e.g., "Mode Shape 1"), then x and y location of the top-left corner of the window (relative to the upper-left corner of the screen), and finally width and height of the graphical window in pixels. Projector reference point (prp) is defined next. This point defines the center of projection (viewer's eye)(for more information: Viewpoint Projections and Specifications). Usually it is placed at the center of the object that is to be graphically presented. For this example, the center of the structure is at (h,h), h being the height of the column (Figure 1). Next, we have to define view-up (vup) vector and view-plane normal (vpn) vector. They are (0,1,0) and (0,0,1), respectively. Window view is defined next using command viewWindow and the four coordinates (-x, x, -y, y) that define the size of the viewing window relative to the prp. In this example h is 144, so the viewing window with its vector (-200, 200, -200, 200) is set to have 56 units of blank space all around the structure. Finally, we use display command to display the mode shapes. The first argument following the command specifies the type of response to be plotted (e.g., -1 is tag for displaying the 1st mode shape, -2 is the tag for displaying the 2nd mode shape, and so on). The second argument following display command is magnification factor for nodes and the third argument is magnification factor for the response quantity to be displayed.
recorder display "Mode Shape 1" 10 10 500 500 -wipe prp $h $h 1; vup 0 1 0; vpn 0 0 1; viewWindow -200 200 -200 200 display -1 5 20 recorder display "Mode Shape 2" 10 510 500 500 -wipe prp $h $h 1; vup 0 1 0; vpn 0 0 1; viewWindow -200 200 -200 200 display -2 5 20